Плоские прямоугольные геодезические координаты

Для решения многих задач гораздо удобнее и практичнее перейти от геодезических координат В и L к системе плоских прямоугольных геодезических координат X, Y. При этом должна быть обеспечена однозначная связь геодезических и плоских прямоугольных геодезических координат точек (в дальнейшем плоских прямоугольных координат). Указанной цели достигают, если поверхность общего земного эллипсоида (референц-эллипсоида) изобразить на плоскости по соответствующим математическим правилам, которые образуют так называемые «картографические проекции».

Аналитически картографические проекции описывают соответствующими математическими уравнениями, позволяющими определить по геодезическим координатам точки (В, L) ее плоские прямоугольные координаты (X, Y) в соответствующей картографической проекции. Отметим важное обстоятельство - отобразить поверхность эллипсоида на плоскости без искажений невозможно. По характеру искажений картографические проекции могут быть равноугольными, равновеликими и произвольными.

Основное условие равноугольного отображения поверхности эллипсоида на плоскости - подобие бесконечно малых фигур, что обуславливает отсутствие при переходе от поверхности эллипсоида на плоскость искажений углов малых геометрических фигур. В равновеликих картографических проекциях отношение соответствующих площадей геометрических фигур сохраняется постоянным.

На практике удобно, чтобы меридианы и параллели на картах представляли собой прямые линии. Для этого при преобразовании на плоскость поверхности эллипсоида (шара) используют цилиндрические картографические проекции.

В Российской Федерации для перехода от геодезических координат (В, L) к плоским прямоугольным геодезическим координатам (X, Y) используют поперечную цилиндрическую равноугольную картографическую проекцию, получившую название «проекция Гаусса-Крюгера», а соответствующую ей систему координат называют государственной. Она разработана исходя из следующих условий:

проекция сохраняет равенство соответствующих горизонтальных углов на поверхности эллипсоида и на плоскости;

бесконечно малый контур на эллипсоиде изображается подобным ему контуром на плоскости;

масштаб изображения в каждой точке проекции зависит только от ее координат и не зависит от направления;

при использовании проекции земной эллипсоид разделяется меридианами на зоны, имеющие свое начало координат - пересечение осевого меридиана с экватором;

масштаб проекции вдоль осевого (среднего) меридиана зоны равен единице, т. е. его изображают без искажения.

Осевой меридиан зоны и экватор изображают на плоскости двумя взаимно перпендикулярными линиями.

Принцип построения картографической проекции Гаусса-Крюгера показан на рисунке 1.5. Как отмечалось ранее, при использовании проекции Гаусса-Крюгера в основу положено разделение поверхности общего земного эллипсоида на ряд одинаковых меридианных полос с заданной разностью долгот 6º граничных меридианов. Изображение на плоскости каждой шестиградусной полосы представляет собой колонну листов Международной карты мира в масштабе 1:1000000

1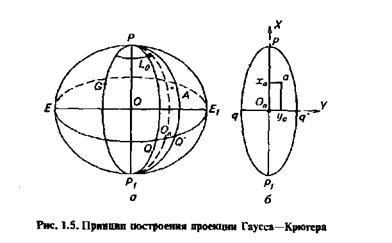

Шестиградусная полоса в свою очередь является шести градусной координатной зоной, ограниченной изображениями соответствующих меридианов. В зоне с номером n (рис. 1.5, а) кривые PQP_} и PQ'P₁ являются граничными меридианами 6° зоны; пунктирная линия - осевой меридиан, долгота которого L₀ = 6º n- 3 °. Эта зона на плоскости изображена в проекции. Кривые pqp_] и pq'p₁ - изображения граничных меридианов; прямая рр₁ - изображение осевого меридиана, а прямая qq' - изображение экватора. Прямолинейное изображение осевого меридиана и экватора на плоскости позволяет их использовать в качестве осей плоской прямоугольной системы координат. Ось ординат Y направлена на восток и совмещена с изображением линии экватора, а ось абсцисс X совмещена с изображением линии осевого меридиана зоны и направлена на север. Если а - изображение точки А на плоскости, то ее положение определяется плоскими прямоугольными координатами х_а и у_а (см. рис. 1.5, б).

Каждую шестиградусную зону нумеруют арабскими цифрами. На территории Российской Федерации принята нумерация зон, отличающаяся от нумерации зон мировой карты масштаба 1: 1000000 на тридцать единиц, т. е. крайняя западная зона с долготой L₀ осевого меридиана, равной 21º, имеет номер 4, а к востоку номера зон возрастают (до 32-й на Чукотке).

Системы плоских прямоугольных геодезических координат каждой координатной зоны совершенно идентичны. Из этого следует, что плоские прямоугольные координаты X и Y, вычисленные по геодезическим координатам В и L, в любой координатной зоне имеют одни и те же значения. Данное обстоятельство обусловлено тем, что проекция Гаусса-Крюгера является симметричной относительно оси абсцисс. При этом абсциссы точек, имеющих одинаковую широту, являются функциями не долгот, а разностей между ними и значением долготы осевого меридиана. Две точки А и В с одинаковой широтой и с одинаковой разностью долгот относительно осевых меридианов соответствующих зон (рис. 1.6) после их изображения на плоскости имеют одинаковые абсциссу и абсолютное значение ординаты

Чтобы исключить из обращения отрицательные ординаты и облегчить использование плоских прямоугольных координат, ко всем ординатам добавляют постоянное число 500000м. Кроме того, чтобы знать, к какой координатной зоне относятся.плоские прямоугольные координаты точки, к ординате слева приписывают номер зоны. В результате получают число, представляющее собой условную ординату. Например, условная ордината точки, равная 21349821, 425 км, означает, что точка с этой ординатой расположена в 21 зоне, ее действительная ордината -150178,575км, а долгота осевого меридиана зоны L₀ = 6º n- 3 ° = 123°.

Ввиду обособленности систем координат каждой зоны возникают некоторые неудобства в местах их стыковки. В этих случаях для описания положения точек используют системы координат обеих смежных зон.

Положение точки Л расположенной на одном и том же граничном меридиане двух смежных координатных зон, показано на рисунке 1.7. Допустим, что ее геодезические координаты равны соответственно В_Р и L_Р. После изображения данной точки на плоскости ее плоские прямоугольные координаты в системе координат первой (на рис.1.7 - «правой») зоны будут Х_Р1 и Y_P1. Эта же точка во второй системе будет иметь координаты Х_Р2 и Y_P2. Примем, что координаты Х_Р1 и Y_P1 известны и требуется вычислить координаты точки Р в системе координат второй зоны, это часто требуется на практике. Переход от системы координат с одним осевым меридианам к системе координат с другим осевым меридианом называют «переходом из зоны в зону». В общем случае его осуществляют в такой последовательности. Вначале по известным плоским прямоугольным координатам Х_Р1 и Y_P1 вычисляют геодезические координаты В_Р1 и L_Р1.. Затем с учетом разности долгот осевых меридианов соответствующих зон, используя найденные геодезические координаты, вновь определяют плоские прямоугольные координаты Х_Р2 и Y_P2 точки Р, но во второй, т. е. «левой» зоне, изображенной на рисунке 1.7.

Дата добавления: 2014-01-04