Устойчивость линейных многомерных систем

Два вида устойчивости представляют интерес. Первый вид относится к способности системы возвращаться в прежнее состояние равновесия после устранения причины, вызвавшей это отклонение, а другой вид относится к способности системы вырабатывать ограниченный выходной сигнал как реакцию на ограниченный входной сигнал.

Устойчивость первого вида: устойчивость по начальным условиям. Способность предварительно невозбужденной системы возвращаться в нулевое состояние равновесия (устойчивость по начальным условиям) связана с ее свободным движением.

Реакция системы

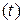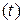y = y_св +y_вын ,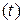

Если u 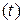= 0, то

.

Определение. Линейная многомерная система называется устойчивой по начальным условиям, если ее свободное движение с течением времени затухает, т.е. если

,

и неустойчивой в противном случае.

Так как при u (t)=0 , то условие устойчивости можно записать как

.

Здесь 0 –нулевой n -вектор.

Переходная матрица состояния 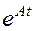, как показано в параграфе 1.3, определяется соотношением

.

Следовательно,

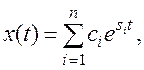
где c_i=E_ix₀ – n - векторные постоянные коэффициенты.

Как видно из последнего выражения, условие устойчивости будет выполняться, если

.

Вывод. Многосвязная система устойчивая, если все собственные значения s_i матрицы системы А (другими словами, корни характеристического уравнения системы ) имеют отрицательную вещественную часть. Отсюда, независимо от того, как велико начальное состояние, при 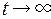. Такую систему называют часто асимптотически устойчивой.

Легко показать, что это условие устойчивости справедливо и для случая кратных собственных значений.

Устойчивость второго вида: устойчивость «ограниченный вход – ограниченный выход» определяется с помощью введения понятия норм векторных сигналов и «коэффициента усиления» многомерной системы.

Каким образом измерить величину векторного сигнала ? Это можно сделать с помощью нормы (вещественного числа), обозначаемой и которая для всех и 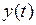обладает свойствами:

Норма есть путь измерения величины сигнала . Наиболее часто используется 2-норма (L ₂- норма или квадратичная норма или «энергия» сигнала):

.

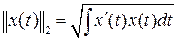Функциональное пространство сигналов с конечной нормой, 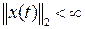, обозначается L ₂ и называется пространством эль два.

Пример. Рассмотрим векторный сигнал с двумя элементами

.

Квадрат второй нормы L ₂- нормы определяется как

Энергия сигнала (квадрат нормы) равна , а его L ₂- норма равна .

Также применяют бесконечную норму ( - норма или максимальное значение сигнала во времени):

где - i -й элемент сигнала .

Обобщим понятие коэффициента усиления усилительного звена на многомерную, как статическую, так и динамическую систему. Пусть S – оператор системы (рис. ниже), связывающий два сигнала выход y (t) и вход u (t):

.

Коэффициент усиления (L ₂ - индуцированная норма оператора или норма оператора, индуцированная нормами и ) для этой системы определяется как самое большое возможное (верхняя граница) отношение между нормой выхода и нормой входа для всех входных сигналов, являющихся элементами L ₂-пространства при нулевых начальных условиях,

. (*)

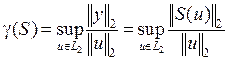Дата добавления: 2014-01-04