Установившаяся реакция многомерной системы

Рассмотрим систему, описываемую в переменных состояния

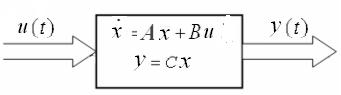
Мы показали, что

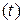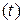y =y_св +y_вын .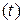

Если система устойчивая по начальным условиям, то

y 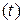=y_пер 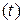+y_уст ,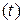

причем переходной процесс y_пер 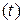затухает, т. е.

,

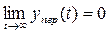а установившийся процесс описывается выражением

, (*)

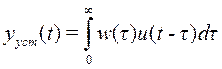где 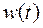- матричная весовая функция.

Рассмотрим два случая:

1. Пусть входной сигнал u (t) – векторный гармонический сигнал, записанный в показательной форме

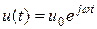, (1)

где постоянный вектор 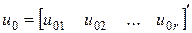- векторная амплитуда гармонического сигнала, 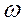- частота гармонического сигнала.

Найдем установившуюся реакцию: y_уст -?.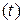

Подставим (1) в (*), получаем

,

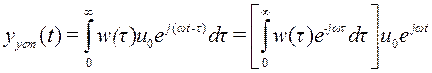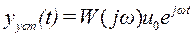, (2)

где матрица ()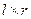

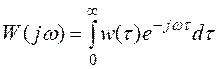
- матричная АФХ многомерной системы.

Так как матричная ПФ определяется как

,

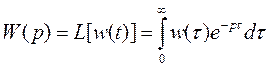то

.

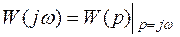Заметим, что мы не можем построить годограф 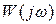для многомерной системы в отличие от одномерной, потому что 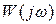- матрица.

Введем понятие скалярных АФХ. Запишем матричную АФХ в символической форм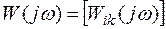е , где 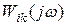- (i, k)-ый элемент 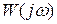. Напомним, что матричная ПФ

, ,

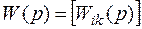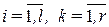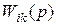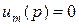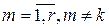где - скалярная ПФ, связывающая преобразование Лапласа i –го выхода с преобразованием k –го входа, так что,если ,,то

.

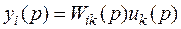Следовательно, скалярная АФХ связана со скалярной ПФ как

.

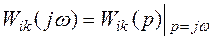Отсюда можно выяснить физический смысл скалярной АФХ: 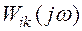определяет установившуюся реакцию, получаемую на i -том выходе при подаче на k -й вход гармонического сигнала, при этом сигналы на остальных входах отсутствуют и система предварительно невозбуждена, т. е.

,

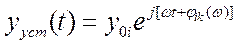где

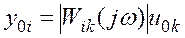- амплитуда установившейся реакции на i -ом выходе,

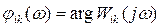- фаза установившейся реакции на i -ом выходе.

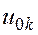- амплитуда гармонического сигнала на k -ом входе.

2. Пусть входной сигнал u (t) - постоянный вектор

.

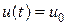Найдем y_уст(t), используя 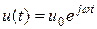(1) и 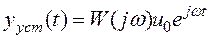(2). Так как постоянный вектор можно рассматривать как частный случай гармонического сигнала при 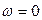, то установившаяся реакция

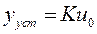
представляет собой постоянный вектор. Здесь

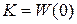
- матричный коэффициент усиления многомерной системы.

В символическом виде:

,

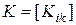где

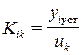- скалярный коэффициент усиления.

Ранее показали, что ПФ определяется как 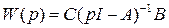. Следовательно, матричный коэффициент усиления

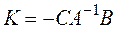
определяется посредством А, В, С.

Дата добавления: 2014-01-04