Лекция 9

Заметим, что если известны статистические характеристики шума измерения и возмущений, приложенных к объекту, то можно построить оптимальный наблюдатель, фильтр Калмана-Бьюси (см. далее).

Итак, решение задачи по выбору вектора связано с размещением полюсов наблюдателя, другими словами, собственных значений матрицы

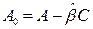
на комплексной плоскости p.

Но здесь возникает вопрос, всегда ли можно путем выбора векторного коэффициента добиться желаемого, в общем случае произвольного расположения собственных значений матрицы 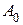? Для ответа на этот вопрос, прежде всего, заметим, что собственные значения матрицы и соответствующей ей транспонированной матрицы

совпадают. Отсюда задачу размещения собственных значений матрицы или, другими словами, полюсов наблюдателя для исходного объекта (1) можно решать как задачу размещения собственных значений матрицы 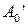с помощью вектора .

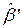Последняя задача в свою очередь в математическом плане эквивалентна определению вектора обратной связи по состоянию 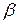в задаче размещения полюсов системы, рассмотренной в предыдущем параграфе.

Задачу размещения полюсов системы можно рассматривать как следующую абстрактную задачу.

Даны матрицы A и B.

Требуется найти такой вектор 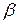, чтобы матрица 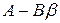имела собственные значения 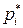. Эта задача имеет решение при условии, что объект управления полностью управляем, т.е. если

,

где

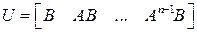— матрица управляемости объекта.

Задача размещения полюсов наблюдателя в абстрактном виде.

Даны A ’ и С ’.

Найти такое 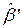, которое обеспечит любое расположение полюсов матрицы

.

Следовательно, данная задача разрешима, если матрица

,

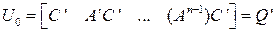получаемая из матрицы путем замены A на A ’, B на С ’, имеет

.

Здесь Q – матрица наблюдаемости объекта. Итак, с помощью 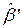можно обеспечить любое расположение полюсов наблюдателя, если

.

При этом исходный объект (1) полностью наблюдаем. Отсюда вывод: если объект управления полностью наблюдаем, то можно гарантировать желаемое качество протекания переходного процесса в наблюдателе выбором вектора .

Так как задача отыскания подходящего для наблюдателя эквивалентна определению коэффициента обратной связи в задаче размещения полюсов системы, то вектор можно найти, воспользовавшись любым из приведенных в предыдущем разделе методом, при этом изменив обозначения на , U на Q ’, A на A ’. Так, из формулы Аккермана следует, что определяется выражением

,

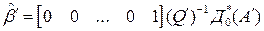где

.

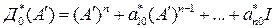Здесь есть коэффициенты желаемого многочлена наблюдателя ,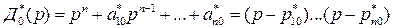

определяемые требуемыми значениями его полюсов.

При этом говорят, что задача размещения полюсов наблюдателя дуальна задаче размещения полюсов системы.

В простых задачах легче всего ввести вектор с неизвестными компонентами 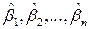и записать условия равенства коэффициентов характеристического многочлена наблюдателя заданным величинам в виде системы уравнений относительно .

Пример 3. Пусть объект управления представляет собой двойной интегратор и описывается уравнениями

, ,

так что

,

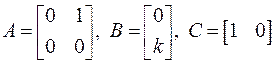При этом n= 2 и согласно (3) 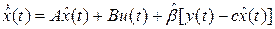наблюдатель полного порядка характеризуется моделью

.

Матрица наблюдателя в соответствии с (7) имеет вид

.

Следовательно, характеристический многочлен наблюдателя

.

Если задан желаемый характеристический многочлен наблюдателя , то из условия находим требуемые значения элементов вектора : .

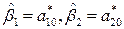Команда Matlab: .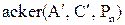

Дата добавления: 2014-01-04