Системы, имеющие неустойчивые обратные

Читать

Теорема. Цифровая система n -порядка (48) наблюдаема тогда и только тогда, когда матрица наблюдаемости размерностью ()

(49)

имеет ранг n.

Для системы с одним выходом l= 1 матрица Q является квадратной размерностью (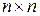), -при этом условии наблюдаемости принимает вид

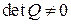. (50)

По своей сути наблюдаемость требует, чтобы каждая переменная состояния оказывала влияние на управляемую величину.

Непрерывная система с рациональной передаточной функцией неминимально-фазовая, если она имеет нули в правой полуплоскости или временное запаздывание. Аналогично цифровая система неминимально-фазовая, если ее нули лежат вне единичной окружности. Это означает, что запаздывание (при этом полюсы) не определяет неминимально-фазовость такой системы в отличие от непрерывной системы. Вместе с тем она не приводит к таким сложнейшим задачам, как в непрерывных системах. Таким образом, в случае цифровых систем целесообразнее говорить о системах с устойчивыми обратными или без них.

Определение неустойчивой обратной системы. Система, обратная к данной цифровой, неустойчива, если она имеет нули вне единичной окружности.

Непрерывная система с устойчивой обратной после дискретизации может стать цифровой системой с неустойчивой обратной. Обратная система всегда неустойчива, если эксцесс полюсов (разность между числом полюсов и нулей) непрерывной системы больше двух, а период дискретизации достаточно мал. Однако непрерывные, неминимально-фазовые системы не всегда становятся цифровыми системами с неустойчивой обратной.

Дата добавления: 2014-01-04