Размещение и занятость

«Размещение» – распределение объектов по ячейкам.

Объекты могут быть любой природы и в любом количестве.

Ячейки – независимо классифицируются по виду, вместимости, числу.

Порядок объектов, вкладываемых в ячейку может учитываться.

Задача о числе возможных способов размещений объектов в заданных ячейках называется задача о размещении.

(Задача о размещении – задача о разбиении элементов на множество классов).

Задача занятости исследует вопрос о числе объектов в заданных или произвольно выбранных ячейках.

Рассмотрим простейших случай:

n различных объектов

m различных ячеек.

Спецификация 1 – на занятость каждой ячейки не положено никаких ограничений.

Проанализируем ситуацию.

а). Первый объект размещается m способами.

б). Второй – m (ничего не изменилось)

объектов

………………………………………….

ячеек

В результате по правилу умножения имеем 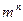способов.

Дано:

2 объекта, 3 ячейки.

1-я 2-я 3-я

1)	-
2)			-
3)	-
Всего 3^2= 9 способов. 4)			-
5)		-
6)		-
7)		-	-
8)	-		-
9)	-	-

Подойдем к этому результату другим путем.

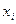- индикатор занятости i -ой ячейки.

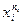- попадание 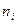элементов в i -ю ячейку.

Распределение единственного объекта по ячейкам примем выражение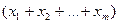

Индикатор распределения n различных объектов

Экспоненциальная производящая функция для последнего случая

Это производящая функция.

После раскрытия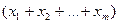

возникают (перечисляются) комбинации вида

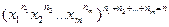
Энемератором занятости i -ой ячейки является

Конкретное число комбинаций получим, положив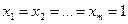

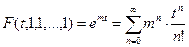
Это соответствует ранее полученным результатам: размещения n объектов по m ячейкам.

II. Рассмотрим число способов размещения n различных элементов по m различным ячейкам при условии, что ни одна ячейка не оказывается пустой.

m

{1} {1} {1}

	-ячеек

………….

вид энумератора

Энумератор имеет вид

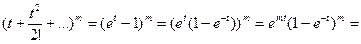
Пусть , тогда ,

n – число объектов m – число ячеек

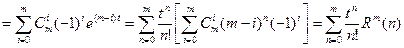
Число способов размещения n различных объектов по m различным ячейкам (ни одна ячейка не пустая!)

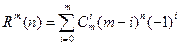
III. Найдем число способов размещения n различных элементов по m ячейкам при условии, что в i -ой ячейке (i =1,2,… m) помещается 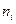элементов

m

{} {} {}

		n объектов
	-ячеек

………….

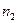Индикатор ситуации

…

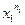
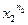есть формула представления полинома

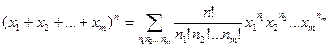
Суммирование идет по различным числам …

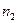Искомое число

См. формулу перестановок n элементов, из которых принадлежит 1-му классу, 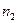- второму, и т.д.

Заключение:

Существует тесная связь размещений с сочетаниями и перестановками (результаты получились аналогичные).

Изучение размещений отличается своей спецификой и потому оправдывает самостоятельное рассмотрение.

Дата добавления: 2014-01-04