
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Статическая устойчивость простейшей системы
|
|
|
|
На рисунке 2.1, а представлены два основных агрегата электрической станции: турбина и генератор.
Ротор турбины приводится во вращение энергоносителем (паром или водой). Вращающий момент турбины зависит от количества энергоносителя. В нормальном режиме эксплуатации основные параметры энергоносителя – стабильны, поэтому вращающий момент турбины постоянен. Мощность, выдаваемая генератором в систему, зависит от характеристики мощности генератора.
Для получения характеристики мощности построена упрощенная векторная диаграмма электропередачи (рис. 2.1,в), которая повторяет диаграмму, изображенную на рисунке 1.3. Из схемы замещения следует, что результирующее сопротивление системы Хdрез= Хd+ХТ1+ХL1//ХL2+ХТ2.
Из векторной диаграммы следует, что
Iа·Хdрез = Е·sinδ,
где Iа - активная составляющая тока;
δ - угол сдвига ЭДС Е относительно напряжения U.
Умножая обе части равенства на U/Хdрез, получим активную мощность, передаваемую приемной системе:
U·Ia = Р = , (2.1)
, (2.1)
где Р - активная мощность, выдаваемая генератором (принята в относительных единицах).
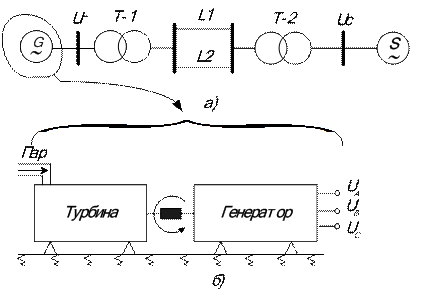
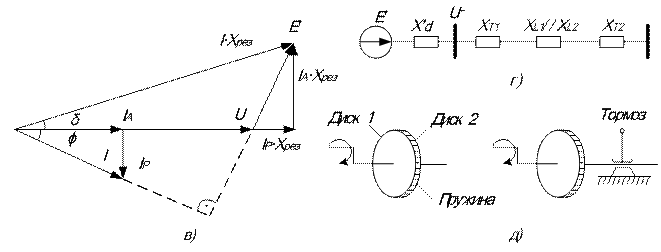
Рис. 2.1. Оценка статической устойчивости простейшей системы: а - принципиальная схема системы; б - блок турбина - генератор; в - векторная диаграмма генератора; г - схема замещения системы; д - механический аналог блока турбина –генератор
Зависимость (2.1) имеет синусоидальный характер и называется характеристикой мощности генератора. При постоянных ЭДС Е генератора и напряжении U угол поворота генератора определяется только его активной мощностью, которая, в свою очередь, определяется мощностью турбины. Наглядной иллюстрацией зависимости мощности (момента) турбины от угла сдвига δ является система двух дисков, соединенных пружинами (рис. 2.1,б). В режиме холостого хода (без учета трения) приводящий (поле ротора, связанного с турбиной) и приводимый (поле статора) диски не образуют угла сдвига относительно друг друга. При появлении тормозящего момента (реакция статора) угол сдвига между дисками будет тем больше, чем больше тормозящий момент. Очевидно, что при увеличении тормозящего момента может произойти проворот одного диска относительно другого, что является нарушением устойчивости рассматриваемой системы.
Мощность турбины зависит от количества энергоносителя и в координатах Р, δ изображается прямой линией.
При определенных значениях ЭДС генератора Е и напряжения приемной системы U характеристика мощности имеет максимум, который вычисляется по формуле
Ртах =  . (2.2)
. (2.2)
Иногда эту величину называют «идеальным» пределом мощности простейшей электрической системы. Заданному значению мощности турбины соответствуют две точки пересечении характеристик а и b (рис. 2.2,а), в которых мощности генератора и турбины уравновешивают друг друга.
Рассмотрим режим работы в точке a. Если мощность генератора по какой-либо причине изменится на величину ΔР, то и угол δ, следуя синусоидальной зависимости, изменится на Δδ. Из рисунка 2.2,а следует, что в точке а положительному приращению мощности соответствует положительное приращение угла. Что же касается мощности турбины, то она не зависит от угла δ и при любых его изменениях остается постоянной и равной Р0.
При изменении мощности генератора равновесие моментов турбины и генератора нарушается. При увеличении мощности генератора на валу, связывающем его с турбиной, возникает избыточный тормозящий момент, поскольку тормозящий момент генератора преобладает над вращающим моментом турбины. Под влиянием тормозящего момента ротор генератора начинает замедляться, что вызывает перемещение ротора и связанного с ним вектора ЭДС 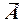 в сторону уменьшения угла δ (рис. 2.2,б). В итоге в точке а восстанавливается исходный режим работы и, как следует из определения статической устойчивости, этот режим является устойчивым. Такой же вывод можно получить и при уменьшении мощности генератора в точке а.
в сторону уменьшения угла δ (рис. 2.2,б). В итоге в точке а восстанавливается исходный режим работы и, как следует из определения статической устойчивости, этот режим является устойчивым. Такой же вывод можно получить и при уменьшении мощности генератора в точке а.
В точке в отрицательному приращению мощности генератора соответствует положительное приращение угла. При уменьшении мощности генератора на валу возникает ускоряющий избыточный момент, который увеличивает угол δ. С ростом угла мощность генератора падает, это увеличивает ускоряющий момент, т.е. возникает лавинообразный процесс, называемый выпадением генератора из синхронизма. Процесс выпадения из синхронизма и асинхронный режим, в котором в итоге оказывается генератор, характеризуются непрерывным перемещением вектора ЭДС 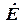 относительно напряжения
относительно напряжения 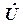 приемной системы (рис. 2.2,в). Если в точке в возникнет тормозной избыточный момент (мощность генератора увеличится), то он вызовет перемещение рабочей точки системы турбина - генератор в точку а.
приемной системы (рис. 2.2,в). Если в точке в возникнет тормозной избыточный момент (мощность генератора увеличится), то он вызовет перемещение рабочей точки системы турбина - генератор в точку а.
Таким образом, точка а характеристики мощности является точкой устойчивого равновесия, точка b - точкой неустойчивого равновесия моментов турбины и генератора. Поэтому все точки, лежащие на возрастающей части характеристики мощности, являются точками устойчивой работы системы, а точки, лежащие на падающей части характеристики, точками неустойчивой работы.
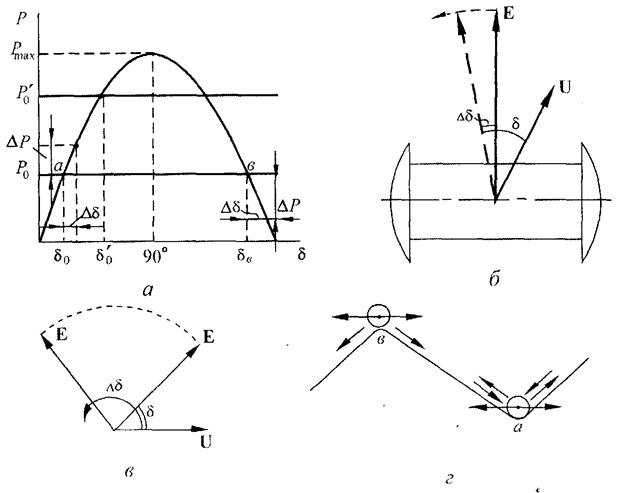
Рис. 2.2. К определению критерия статистической устойчивости простейшей системы: а - характеристика мощности; б - отклонение вектора ЭДС от состояния равновесия; в - выпадение из синхронизма; г - механическая интерпретация
Границей зон устойчивой и неустойчивой работы является максимум характеристики мощности.
Механическим аналогом рассматриваемой системы с точки зрения статической устойчивости может служить шарик, помещенный на изогнутую поверхность так, как это показано на рисунке 2.2, г. Положение точки а устойчиво, так как любое (даже незначительное) перемещение шарика влево или вправо заканчивается его возвращением в исходную точку. Положение в неустойчиво, так как малейшее отклонение от этого положения вызовет переход шарика в новое положение.
Формальным признаком статической устойчивости электрической системы может служить знак приращения мощности к приращению угла. Если  , то система устойчива, если это отношение отрицательно, то неустойчива. Переходя к пределу, можно записать критерий статической устойчивости простейшей системы:
, то система устойчива, если это отношение отрицательно, то неустойчива. Переходя к пределу, можно записать критерий статической устойчивости простейшей системы:
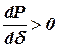 . (2.3)
. (2.3)
Увеличение мощности турбины от значения Р0 до Р0' (рис. 2.2, а) приводит к возрастанию угла ротора до значения δ0' и уменьшению запаса статической устойчивости, который определяется следующим образом:
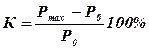 . (2.4)
. (2.4)
Запас устойчивости электропередачи, связывающей станцию с шинами энергосистемы, должен быть не менее 20 % в нормальном режиме и 8% в кратковременном послеаварийном.
|
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 2207; Нарушение авторских прав?; Мы поможем в написании вашей работы!