Анализ сетевых моделей

Решение

Сетевая модель задачи приведена на рис. 12.

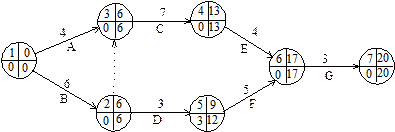
Рис. 12 - Сетевой график задачи

Календарное планирование предусматривает определение сроков начала и окончания каждой работы и других характеристик сетевого графика. Это позволяет проанализировать сетевую модель, выявить критические работы, непосредственно определяющие срок выполнения проекта, провести оптимизацию использования ресурсов (временных, финансовых, исполнителей).

Расчет сетевой модели начинают с временных параметров событий. Их вписывают непосредственно в вершины сетевого графика:

· T_p(i) – ранний срок наступления события i. Это минимально необходимое время выполнения всех работ, которые предшествуют событию i;

· T_п(i) – поздний срок наступления события i. Превышение этого срока вызовет аналогичную задержку наступления завершающего события сети;

· R(i)=T_п(i)-T_p(i) – резерв времени события i. Это время возможной задержки наступления события i без нарушения сроков завершения проекта в целом (рис.13).

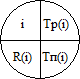
Рис. 13 - Отображение временных параметров событий

на сетевом графике

Ранние сроки свершения событий T_p(i) рассчитываются от исходного (И) к завершающему (З) событию следующим образом:

1) для исходного события И:

;

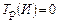2) для всех остальных событий i:

T_p(i)=,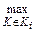

где: T_p(i) - максимальная длительность из всех работ 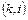, предшествующих событию i;

– длительность работы (k,i) (рис. 14).

Рис. 14 - Расчет раннего срока 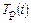свершения события i

Поздние сроки свершения событий рассчитываются от завершающего к исходному событию:

1) для завершающего события З:

;

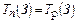2) для всех остальных событий:

,

где: Т_n(i) минимальная продолжительность из всех работ 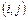, следующих за событием i;

t (i, j) – длительность работы (i, j) (рис. 15).

Рис. 15 - Расчет позднего срока свершения события i

Путь – это последовательность работ в сетевом графике (в частном случае это одна работа), в которой конечное событие одной работы совпадает с начальным событием следующей за ней работы.

Полный путь – это путь от исходного до завершающего события.

Критический путь – максимальный по продолжительности полный путь. Критические работы имеют нулевые свободные и полные резервы. Работы, лежащие на критическом пути, называют критическими.

При поиске критических путей на сетевом графике будем использовать следующие условия его критичности:

· необходимое условие – нулевые резервы событий, лежащих на критическом пути;

· достаточное условие – нулевые полные резервы работ, лежащих на критическом пути.

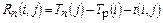· – полный резерв работы показывает максимальное время, на которое можно увеличить длительность работы 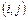или отсрочить ее начало, чтобы не нарушился срок завершения проекта в целом;

· – свободный резерв работы показывает максимальное время, на которое можно увеличить продолжительность работы 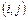или отсрочить ее начало, не меняя ранних сроков начала последующих работ.

Задача 2

Исходные данные по основным операциям приведены в задаче 1. Требуется определить критические пути модели и проанализировать, как влияет на ход выполнения проекта задержка работы D на 4 недели.

Дата добавления: 2014-01-05