Лекция 7. Решение задачи распределения

Классификация задач.

В теории распределения рассматриваются, преимущественно, задачи с независимыми затратами и доходами. Это объясняется не тем, что такие задачи более важны, а лишь тем, что для них значительно легче строить модели и получать решения. Если затраты (или доход), определяемые объемом x_{ij *} c_ij ресурса i, выделенного на выполнение работы j, равны x_ij то мы имеем линейную распределительную задачу

Распределительные задачи с независимыми линейными функциями затрат (или дохода) стали объектом наиболее интенсивных исследований, ввиду того, что для их решения были разработаны эффективные итеративные методы линейного программирования.

Однако имеются также методы решения некоторых нелинейных распределительных задач, в том числе методы, основанные на линейной аппроксимации. Распределение ресурсов для одного периода времени может влиять на распределения ресурсов для последующих периодов, а может не оказывать на них никакого влияния.

Если каждое из последовательности распределений не зависит от всех остальных, то такая задача называется статической, в противном случае - имеем динамическую распределительную задачу.

Статические задачи исследованы в большей степени, чем динамические, но для решения некоторых типов динамических задач успешно применяются методы линейного динамического, или просто: динамического программирования.

Для решения некоторых динамических задач применяют методы стохастического программирования. В таких задачах принятие решений основано на вероятностных оценках будущих значений параметров (например, удельных затрат, продажной цены, спроса и т. д.), имеющих фиксированное распределение вероятностей.

Основные методы решения распределительных задач, в частности, линейное программирование, построены на допущении, что объемы имеющихся в наличии ресурсов (b_i), требуемые объемы (a_j) и затраты (c_ij) точно известны.

появилась раньше второй.

В исследовании операций имеет значение не только выбор модели, но и понимание адекватности её алгоритмов. Это необходимо для формирования решений, которые будут корректно использоваться для повышения эффективности реальных систем.

Учитывая вышеизложенное, обратимся к математическим моделям линейной алгебры, которая подготовила почву для решения сложных задач распределения.

Линейная алгебра - это часть алгебры, изучающая векторные (линейные) пространства и их подпространства, линейные отображения (операторы), линейные, билинейные и квадратичные функции (функционалы или формы) на векторных пространствах.

Но исторически первым разделом линейной алгебры была теория линейных уравнений.

В связи с решением систем линейных уравнений возникло понятие определителя. В 1750 году были получены формулы Крамера для решения системы линейных уравнений, в которой число уравнений равно числу неизвестных и определитель из коэффициентов при неизвестных отличен от нуля.

В 1849 году был предложен метод Гаусса, который используется и в настоящее время для практических исследования и решения систем линейных уравнений.

В связи с изучением систем линейных уравнений и их определителёй появилось понятие матрицы.

Понятие ранга матрицы, предложенное Г. Фробениусом в 1877 году, позволило явно выразить условия совместности и определенности системы линейных уравнений в терминах коэффициентов этой системы. Тем самым, было завершено построение общей теории систем линейных уравнений.

Рассмотрим простейшую систему линейных уравнений с неизвестными:

(5.1)

Где число уравнений не предполагается равным числу неизвестных:

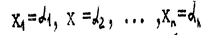
Решением системы называется совокупность определённых значений неизвестных, которые при подстановке обращают уравнения в тождества.

Система, имеющая хотя бы одно решение, называется - совместной.

Система, не имеющая ни одного решения, называется - несовместной.

Система, имеющая единственное решение, называется - определённой.

Система, имеющая более одного решения, называется - неопределённой.

Здесь необходимо заметить, что по внешнему виду системы уравнений классифицировать по названным выше признакам невозможно.

Чтобы осуществить такую классификацию - нужно провести исследование системы уравнений. При этом может быть обнаружено, что одно из уравнений (или несколько) являются линейно зависимыми от остальных, то есть могут быть получены из них путём линейных преобразований (сложением и вычитанием одного или нескольких остальных уравнений и (или) умножением уравнений на постоянные коэффициенты).

Число линейно независимых уравнений системы (при условии их совместности) называется рангом системы.

  (5.2)

Суть математической формулировки задач линейного программирования сводится к определению экстремума линейной функции конечного числа неотрицательных аргументов, связанных между собой системой линейных ограничений, а именно функции следующего вида:

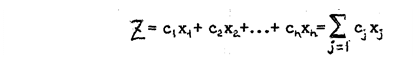
если аргументы связаны системой линейных ограничений, то эту систему можно записать следующим образом:

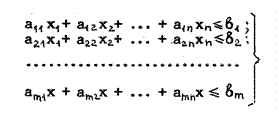
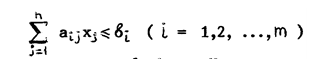
Величины c_i, a_ij, b_i заданы. Число неизвестных x_j равно n, а число

линейных ограничений – m, причём: n ≥ m.

Кроме того, полагают, что отрицательные значения неизвестных не принимаются во внимание, поскольку это не имеет смысла в практических задачах.

Таким образом, необходимо решить систему линейных неравенств (или равенств), и из всех возможных решений выбрать такое, при котором функция Z принимает минимальное (максимальное) значение.

Если, например, речь идёт о расходах, то ищут минимум функции, если моделируются доходы, то задача формулируется как поиск максимума.

Классический пример общей задачи линейного программирования - это задача оптимального распределения ресурсов. Одним из наиболее эффективных методов решения задач является симплекс-метод, основы которого разработал американский математик Данциг в 1947 году.

Сущность метода заключается в последовательном улучшении начального решения задачи (исходного, так называемого опорного плана), построенного по некоторому первоначальному алгоритму.

Однако оптимальное значение в математическом смысле не всегда совпадает с понятием реальной экономической оптимальности.

Например, в так называемой “транспортной задаче”, где имеют место экономические интересы, по меньшей мере, трёх субъектов экономики, полученное математическое решение вряд ли устроило бы всех участников одновременно. В таких случаях прибегают к различным усложнениям задачи, приемлемым для конкретных условий и данных участников.

Исходные данные по поставленной распределительной задаче представлены в виде табличной матрицы (таблица 6.2.)

Таблица 6.2.

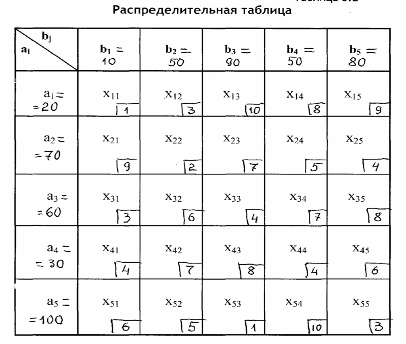
Первичная формализация задачи в табличной матрице содержит:

в левом обрамляющем столбце (сверху-вниз) - количество наличных ресурсов у каждого отправителя груза; в верхней обрамляющей строке (слева-направо) – указаны потребности в ресурсах у каждого покупателя; в уголочках справа и внизу каждой клетки, где обозначены корреспонденции грузов, записаны стоимости перевозок единицы груза от отправителя к получателю («единичные стоимости»).

Плату получает перевозчик груза: предполагается, что он заинтересован в снижении себестоимости перевозок для своей клиентуры.

Дата добавления: 2014-01-05