Формулировка задачи

Лекция 8 Постановка задачи линейного программирования

Как уже нами отмечалось ранее, суть математической формулировки задач линейного программирования сводится к определению экстремума линейной функции конечного числа неотрицательных аргументов, связанных между собой системой линейных ограничений, а именно функции следующего вида:

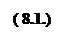
Содержательная формулировка транспортной задачи выглядит следующим образом.

Пусть в пунктах А₁, А₂,..., А_m производится некоторый однородный продукт, причём, объём производства этого продукта в пункте A_i ‚ составляет а_i единиц,

i = 1,..., m.

Произведённый в пунктах производства продукт требуется доставить в пункты потребления В₁, В₂,..., В_n, причём объём потребления в пункте В_j составляет Ь_j единиц продукта.

Предполагается, что транспортировка готовой продукции возможна из любого пункта производства в любой пункт потребления и транспортные издержки, приходящиеся на перевозку единицы продукта из пункта А_i в пункт В_j, составляют a_i денежных единиц, i =1,...,m.

Задача состоит в организации такого плана перевозок, при котором суммарные транспортные издержки были бы минимальными.

Формальная постановка «транспортной задачи».

Пусть x_{ij -} количество продукта, перевозимого из пункта А_i в пункт В_j. Требуется определить совокупность из mn величин х_ij», удовлетворяющих условиям:

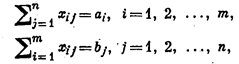
и обращающих в минимум линейную форму:

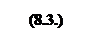
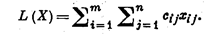
Для решения «транспортной задачи» воспользуемся симплекс–методом, (« симплекс» - в переводе означает «простой», то есть несложный).

Суть метода состоит в приведении задачи к так называемому стандартному виду, при котором обеспечивается равенство ресурсов и потребностей. При этом используется табличная матрица, которая была уже нами представлена в лекции 6 (табл.6.1.)

Все преобразования симплекс-метода мы также будем проводить непосредственно в табличной матрице. Каждое очередное преобразование (итерация, что в переводе означает «шаг») будет продуцировать новый план перевозок, с уменьшенным значением целевой функции. Преобразования-итерации заканчиваются достижением оптимума. Для этого используются два метода: распределительный метод и метод потенциалов.

Каждый из названных методов приводит к оптимальному решению.

Каждый из алгоритмов по названным двум методам начинается спостроения опорного решения, оно является исходным, с которого начинаем реализацию алгоритма. Нахождение опорного решение строится образом, что, в нём число заполненных клеток должно равняться рангу системы r

r = p+ q – 1 (8.4)

Для нахождения опорного решения имеются два метода: метод северо-западного угла и метод минимального элемента.

При этом формулируются и следующие ограничения:

- значения переменных х должны быть больше или равны нулю, поскольку отрицательными объёмы перевозок быть не могут;

- остаётся в силе приведенное определение ранга системы.

Заметим, что общее число базисных решений, которые, могут удовлетворять записанным уравнениям составляет N_б

где:

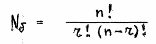
здесь: n - общее число переменных x

r – ранг системы.

Если мы найдём все базисные решения данной системы, то среди них окажутся и такие, в которых базисные переменные будут положительными.. Такие решения называют опорными решениями. При проведении итераций в распределительной таблице следует помнить, что нули базисных переменных обязательно записываются в свободные клетки, в отличие от нулей свободных переменных, которые имитируются пустыми клетками.

Обычно такие базисные нули фигурируют в угловых клетках цикла, и без их использования невозможно организовать целенаправленного циклического преобразования. В целом методика решения данной задачи осуществляется в следующей последовательности: 1. Находим одним из двух методов исходное опорное решение системы, 2. Осуществляем цепочку последовательных циклических преобразований опорного решения симплекс-методом, достигая уменьшения целевой функции. З. Останавливаем процесс при достижении Z _min.

8.2.Нахождение опорного решения методом «северо-западного угла».

Сущность метода поясним на примере решения (табл. 8.2.1).

Метод северо-западного угла Таблица 8.2.1

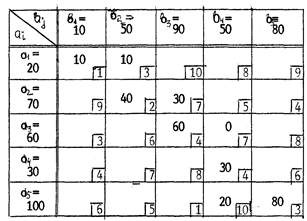
Z₁ = 1130

Процесс распределения ресурсов начинается с клетки, расположенной на «северо-западе», то есть в левом верхнем углу. Ей соответствует ресурс а₁ = 20 и

потребность b₁ = 10. Удовлетворяем потребность полностью, остаётся ресурс, равный 10. Теперь, по правилу, “дораспределяем» остаток ресурса, передав его следующей потребности b₂ которая его забирает, но с нехваткой относительно её потребности. Нехватка ресурса для потребности b₂ восполняется уже за счёт ресурса a₂, расположенного, уже, во второй строчке таблицы. Действия повторяются таким же образом и далее, с образованием ряда ступенек, ведущих в правый нижний угол, где и заканчивается процесс начального распределения.

При нахождении опорного решения данным образом следует иметь в виду, что иногда на некоторой клетке таблицы одновременно заканчиваются и ресурсы, и потребности. Тогда для дальнейшего продвижения (по правилам расчёта) записывается базисный ноль -либо в последующей клетке той же строчки, либо в последующей клеточке того же столбца.

В законченном расчёте любого опорного решения количество заполненных клеток должно быть равно рангу системы минус единица. В противном случае, реализация алгоритма нахождения опорного решения становится невозможной.

Как первое, так и все последующие решения являются возможными для практического осуществления, а эффективность каждого оценивается значением целевой функции. Целевая функция практически служит критерием эффективности того или иного плана, записанного в виде корреспонденций груза в каждой клеточке распределительной таблицы.

Дата добавления: 2014-01-05