Описание алгоритма однократного замещения

Опорного решения.

Лекция 9 Алгоритм циклических преобразований

Распределительная таблица фактически является матрицей, с которой можно проводить преобразования и получать новые опорные решения используя метод однократного замещения Жордана-Гаусса, сущность которого сводится к назначению другой базисной переменной, вместо одной из свободных.

При таком замещении свободная переменная объявляется базисной и подлежит определению, а некоторая базисная (безразлично какая) становится свободной. В математике доказано, что в каждом опорном решении задачи линейного программирования, размещённом в распределительной таблице, можно построить цикл, (и притом только один), однократного замещения одной свободной переменной на одну базисную переменную. При этом продуцируется новый опорный план с новым значением целевой функции. Матрица «единичных стоимостей», обеспечивает общий расчёт затрат по любому полученному решению. То есть она обеспечивает оценку решения записанного в таблице.

При целенаправленном преобразовании начальной таблицы-матрицы можно достигать как минимизации затрат. Рассмотрим методику названного алгоритма.

Циклом называют набор клеток, в котором две и только две клетки расположены в одной строке или в одном столбце, причём, последняя клетка столбца образует первую клетку строки, и так далее, вплоть до замыкания цепочки в цикле (см. табл. 9.1.1).

Таблица 9.1.1.

Схема циклического преобразования

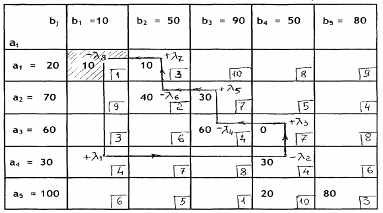
Z₀= 1130

С каждым опорным решением можно провести циклическое преобразование, которое всегда начинается в одной из свободных клеток, затем проходит только через занятые клетки, и заканчивается на исходной клетке.

Число вариантов таких преобразований равно числу свободных клеток. Число занятых клеток всегда должно быть равно рангу системы.

Приводим пример проведения циклического преобразования со свободной клеткой 4-1 (координаты клеток определяются номерами индексов переменных)

Выполним сначала расчёт целевой функции исходному решению Z₀:

Z₀ = 10 · 1 + 10 · 3 + 40 · 2 + 30 · 7 + 60 · 4 + 0 · 7 + 30 · 4 + 20 · 10 + 80 · 3 = 1130

Далее, в порядке знакомства с методом однократного замещения, выберем любую свободную клетку, например, клетку 4-1, построим «от неё» схему цикла

однократного замещения, изобразив его в таблице найденного ранее исходного («нулевого») варианта опорного решения.

В свободной клетке (4-4) размещаем + λ₁ ( первая нечётная порядковая клетка). Протягиваем далее от неё стрелку до занятой клетки (4-4), где будет размещаться - λ₂... далее поступаем аналогичным образом, чередуя положительные и отрицательные значения λ_m, размещённые в угловых клетках, согласно последовательности построения цикла. Заметим, что индексы фиксируют только порядковое расположение λ, и к его численному значению никакого отношения не имеет. Численное значение λ определяется после построения цикла. Правила построение циклов всегда обеспечивают равное количество отрицательных и положительных по знаку значений λ_{m ..}

Использование алгоритма оптимизации Для выполнения очередного циклического преобразования достаточно выбрать клетку, которая, в построенном начальном цикле, имеет наименьшее, (по абсолютной величине), значение переменной, и находится в углу цикла со знаком «минус». В нашем примере это клетка 1-1 в табл. 9.2.1.

Таблица 9.2.1

Дата добавления: 2014-01-05