Распределения вероятностей

Равномерное распределение случайной величины было исторически первым стимулом к исследованию вероятностных процессов, поскольку на его основе возник метод статистических испытаний.

Статистические испытания предполагают многократное повторение однотипных испытаний. Результат любого отдельного испытания случаен и, сам по себе, какого-либо интереса не представляет.

В то же время совокупность большого числа подобных результатов оказывается весьма полезной. Она обнаруживает определенную устойчивость (ее называют статистической устойчивостью), которая позволяет количественно описать явление, исследуемое в данных испытаниях.

Понятие устойчивости испытаний является фундаментальным для теории вероятностей, поскольку оно применимо к исследованиям объективных реальных процессов. Но парадоксальным в этой картине является то, что сама по себе регистрация сведений об устойчивых (в вероятностном смысле) проявлениях процессов не даёт никакой информации, почему так происходит.

Причинно-следственные зависимости, как это не покажется странным, лежат вне компетенции теории вероятностей. Путь к использованию теории вероятности проложен через гипотезу, что изучаемое явление действительно

может быть обобщено численными характеристиками (критериями) теории вероятностей. В отношении самой реальности утвердилось мнение, что во многих массовых процессах складываются вполне устойчивые закономерности, которые могут быть, с пользой для дела, обобщены методами теории вероятностей.

В названных реальных процессах складывается некоторая устойчивая группа основных факторов, которая и обеспечивает конкретные вероятностные свойства реальных процессов.

Равномерное распределение плотности вероятностей, впервые было использовано в игорных домах. Идеально простое, идаже примитивное, устройство рулетки исключало всякую подтасовку результатов игры.

Заметим, что это физическое устройство легло в основу имитационного моделирования, в котором, как раз, и используется физическое равномерное распределение, которое можно трансформировать в другие виды распределений расчётным путём.

Таким образом, возникла возможность имитации реальных процессов путём использования результатов статистических испытаний.

Второе, и более употребительное название такого способа имитации реальных процессов «метод Монте-Карло».

Конечно, город Монте-Карло никакого отношения к разработке метода не имеет. Город Монте-Карло (столица княжества Монако), прославился своими игорными домами и рулеткой. А рулетка является идеальным средством для физической генерации значений случайной величины с равномерным распределением плотности вероятностей.

Приведём пример практического использования равномерного распределения. Функцией распределения двумерной случайной величины

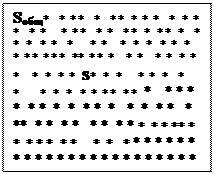(X, Y) называют функцию F(x,y ),

y a определяющую для каждой пары чисел x, y ,

вероятность того, что X примет значение,

меньшее x, и при этом Y примет значение,

меньшее y. Преобразуя генерации значений

b случайной величины, распределённые от

нуля до единицы, всегда можно выполнить

равномерно заполнение некоторого контура

равномерно размещёнными точками, как

это показано на рис.15.4.4. Представим себе

задачу, в которой необходимо вычислить

площадь s, внутри замкнутого контура,

Рис. 15.4.4.График распределения прямоугольника площадью S_общ.

двумерной случайной величины (X, Y). (Площадь S_общ = а × b)

Зная общую площадь S_общ прямоугольника, которая легко вычисляется, можно определить площадь s криволинейного контура: s = (n/N)S_общ , где n – число точек, попавших внутрь криволинейного контура, N – общее число точек, генерированных для решения данной задачи.

Предполагается, что координаты точек криволинейного контура известны: они вводятся в программу расчёта как исходные данные. Координаты каждой очередной генерируемой точки также известны.

Остаётся ввести в программу счётчик общего количества генерируемых точек, и выделить в счёте точки, которые при проведении программной операции сравнения относятся к точкам, попавшим внутрь контура

Дата добавления: 2014-01-05