Исследование характеристик потоков

Необходимость в исследовании характеристик реальных потоков связана с тем, что реальные условия работы систем массового обслуживания сильно отличаются от теоретических их моделей. Благодаря длительной практике использования теории массового обслуживания были установлены правила корректного использовании математических моделей и правила корректирования результатов.

В первую очередь подлежат исследованию входящий поток.

Всякое исследование в теории массового обслуживания начинается с изучения того, что необходимо обслужить, т. е. входящего потока требований. Большинство транспортных потоков удовлетворительно описывается законами распределения: Пуассона, Эрланга, биномиальным, нормальным.

Поток требований, описываемый законом Пуассона, рассматривается как простейший, если он обладает свойствами стационарности, ординарности и отсутствием последействия.

Свойством стационарности обладает поток, у которого вероятность поступления определенного числа требований в течение принятого промежутка времени зависит только от величины этого промежутка и не зависит от того, где на оси времени он находится.

Поток ординарен, если практически не совмещаются в прибытии два и более требований на обслуживание.

Отсутствие последействия заключается в том, что вероятность поступления за период [ t_0, t₀ + t₁ ] числа требований не зависит от того, сколько их? и как они поступали до момента t₀.

Для простейшего потока вероятность того, что за отрезок времени t поступит m требований, равна:

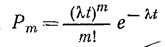
где λ — средняя интенсивность потока требований, измеряемая числом требований, поступивших в единицу времени.

Важная характеристика потока — закон распределения длины промежутка времени T между соседними требованиями. Если этот поток не обладает последействием, то поступление одного требования не влияет на поступление других требований в дальнейшем. Поэтому вероятность того, что интервал между требованиями будет не меньше величины t

Во вторую очередь подлежит анализу поток обслуживания.

Важное понятие теории массового обслуживания — время обслуживания (то есть его продолжительность).

Оно, прежде всего, характеризует функционирование каждого аппарата обслуживающей системы. Продолжительность обслуживания требований может быть различной, что объясняется их неидентичностью, состоянием и техническими возможностями аппаратов, используемых для обслуживания.

В общем случае время обслуживания — это случайная величина, которую описывает закон распределения:

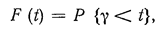
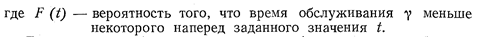
В транспортных системах наибольшее распространение получили показательное и нормальное распределение (рис. 16.2.1).

Функцию распределения времени обслужи- вания, чтобы отличить ее от функ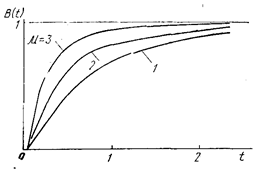ции распределения вероятностей входящего потока, обозначают обычно символом В (t), и при показательном законе распределения

он имеет, вид:

Физический смысл параметра μ — это интенсивность обслуживания, то есть, количество требований, обслуживаемых в единицу времени. Величина, обратная ему, 1/μ — среднее время обслуживания.

Не меньшее значение, чем изучение входящего потока, представляет собой исследование выходящих потоков, т. е. потоков требований после обслуживания.

Особенно это важно, когда поток выходит из одной системы в очередь другой, последовательно соединенной с первой.

Например, выходящим потоком из системы технического осмотра в парке приема сортировочной станции служат моменты окончания осмотра составов. Они же образуют входящий поток в систему расформирования поездов.

В результате обслуживания входящий поток требований подвергается некоторой трансформации, его параметры изменяются.

Основным при этом следует считать степень загрузки обслуживающего аппарата. Если она приближается к единице, то распределение выходящего потока близко к распределению времени обслуживания. Если же предположить, что загрузка аппарата стремится к нулю (при постоянной интенсивности поступления требований продолжительность их обслуживания близка к нулю), то распределение выходящего потока примерно соответствует распределению входящего потока. Коэффициент вариации выходящего потока при произвольных: входящем потоке и времени обслуживания - можно с достаточной степенью

точности можно определить по формуле:

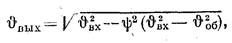
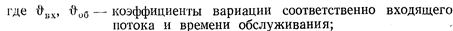
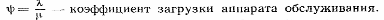
В общем случае распределение выходящего потока — функция трех величин: входящего потока, продолжительности обслуживания и загрузки аппаратов обслуживания.

Дата добавления: 2014-01-05