Массового обслуживания

Фактическое выполнение процессов осуществляется путём реализации конкретного управления. Например, в случае, когда занято устройство обслуживания, то оператор процесса принимает решение по недопуску нового объекта, с которым надо проводить обслуживание. Он вовсе не подчиняется математическому алгоритму, который был разработан в предположении, что все ситуации «продолжают своё соответствие» некоторым теоретическим гипотезам о распределении вероятностей.

Имитационная модель не имеет таких ограничений. Имитировать можно любой процесс, убедившись даже в минимальном сохранении его стабильности на короткую перспективу.

Устойчивость процесса, в принципе, никак не связана с теорией вероятности, поскольку могут быть устойчивыми и процессы, для которых неприменимы формализации теории вероятностей.

В имитационном моделировании может быть использован кибернетический подход, при использовании которого вероятностная модель может рассматриваться как частный случай.

Многоэлементные кибернетические с и с т е м ы строятся из набора (обычно конечного) М элементов путём отождествления выходных сигналов одних элементов с входными сигналами других. Формально такие отождествления задаются системой равенств:

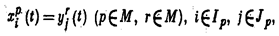
где: через х^p_i(t) обозначена i-я компонента входного сигнала p- го элемента?

а через у^r_j(t) — j -я компонента выходного сигнала r- го элемента.

Важное значение имеет задача нахождения формальных преобразований кибернетических систем, не меняющих задаваемых ими преобразований (а возможно, и некоторых других инвариантов). Тем самым вводятся различные определения эквивалентности систем, делающие возможными постановку задач оптимизации систем, т. е. задач нахождения в классе эквивалентных систем - системы с экстремальными значениями определяемых на них функционалов.

Перевод описаний кибернетических систем на машинный язык представляет собой достаточно трудоёмкую процедуру.

Поэтому в современные средства машинного эксперимента включаются специальные программы—трансляторы (или интерпретаторы), автоматизирующие перевод на машинный язык описаний систем на специально разрабатываемых для этой цели языках системного моделирования.

Основу таких языков составляют средства (удобные для исследователя) фактического отражения параметров, функций и связей, входящих в описание систем. Сохраняя, как правило, универсальность (т. е. возможность описания произвольных систем), языки моделирования обычно ориентированы на более простое и лёгкое описание систем тех или иных специальных классов.

Кроме того, в языки системного моделирования включаются дополнительные средства для описания процедур, обслуживающих машинный, эксперимент, которые были описаны выше. Разработаны многие десятки универсальных и специализированных языков системного моделирования и основанных на них систем машинного эксперимента.

Во многих системах машинного эксперимента имитационное моделирование дополняется возможностями использования аналитического аппарата тех или иных разделов математики (напр., теории массового обслуживания), а также современных вычислительных методов. В первую очередь это касается различного рода оптимизационных методов: линейного программирования, динамического программирования, градиентных методов, стохастического программирования и других.

Взаимоотношения кибернетики с математикой не ограничиваются одним лишь использованием математических методов. Математика в кибернетике имеет общие объекты исследования. Например, алгоритмы, являющиеся объектом исследования в математической теории алгоритмов, могут рассматриваться в то же время как кибернетические системы и служить для кибернетики не только средством, но и объектом исследования.

Однако подход к изучению этого объекта и, следовательно, возникающие при этом задачи у математики и кибернетики сильно отличаются.

Для математики алгоритм выступает, прежде всего, как одно из фундаментальных понятий оснований математики. Поэтому главная задача состоит в изучении общих свойств этого понятия, для чего необходимо свести его определение к минимальному числу простейших фундаментальных понятий и операций.

Кибернетика ставит своей задачей разработку практически удобных методов синтеза конкретных систем, в том числе и алгоритмов. Эта практическая направленность приводит к необходимости разрабатывать достаточно удобные для пользования процедурно и проблемно ориентированные алгоритмические языки.

Вместо простейшей формы представления информация в виде слов в абстрактном алфавите кибернетики изучают сложные структуры данных, необходимые для эффективной реализации алгоритмов на ЭВМ.

Из вышеизложенного следует, что в имитационном моделировании на основе кибернетической концепции применение вероятностных характеристик рассматривается как частный случай использования проблемно ориентированного языка, а именно языка теории вероятностей, вместе со всеми его «языковыми правилами и ограничениями».

Для представляемой разработки приведенное замечание весьма существенно, поскольку в имитационных моделях полезно рассматривать варианты, которые выходят за рамки теории вероятностей, и такие варианты тоже будут рассмотрены.

Дата добавления: 2014-01-05