Слайд 7

Итак, рассмотрим нашу тригонометрическую функцию 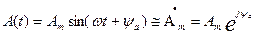представленную в виде комплексной величины на комплексной плоскости. Получается, что наша функция представлена в виде вектора вращающегося на комплексной плоскости против часовой стрелки со скоростью ω, как показано на рис.4.

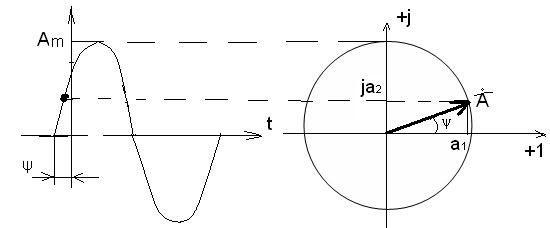
Рис.4

Из рис. видно, что вектор на комплексной плоскости можно построить двумя способами, первый, зная размер вектора и угол, и второй способ, зная координаты вектора по действительной и мнимой осям.

Первый способ это показательная форма представления комплексного числа, т.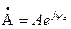е. , где 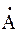- комплексная величина

А- модуль комплексного числа или действующее значение величины

ψ_а- аргумент комплексного числа

Второй способ алгебраическая форма представления комплексного числа:

, где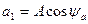

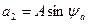
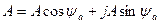
Дата добавления: 2014-01-05