Метод наименьших квадратов

Метод наименьших квадратов позволяет определить коэффициенты уравнения регрессии таким образом, чтобы точки, построенные по исходным данным , лежали как можно ближе к точкам линии регрессии. Формально это записывается как минимизация суммы квадратов отклонений (ошибок) функции регрессии и исходных точек

,

где 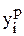– значение, вычисленное по уравнению регрессии; – отклонение (ошибка, остаток); n – количество пар исходных данных.

Простейший вариант модели - прямая линия на плоскости.

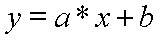
где b - значение y при x=0;
a=tg(α) - тангенс угла наклона прямой по отношению к оси x.

Возможные варианты модели

Анализ отклонений

Первый шаг

Второй шаг

Третий шаг

Четвертый шаг

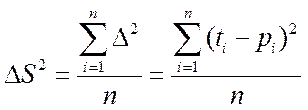
Пятый шаг

Понятие отклонения для случая линейной регрессии

В регрессионном анализе предполагается, что математическое ожидание случайной величины равно нулю и ее дисперсия одинакова для всех наблюдаемых значений Y. Отсюда следует, что рассеяние данных возле линии регрессии должно быть одинаково при всех значениях параметра X. В случае, показанном на рисунке, приведенном ниже, данные распределяются вдоль линии регрессии неравномерно, поэтому метод наименьших квадратов в этом случае неприменим.

Неравномерное распределение исходных точек вдоль линии регрессии

Основная задача корреляционного анализа

Основная задача корреляционного анализа – оценка тесноты (силы) корреляционной связи. Теснота корреляционной зависимости Y от X оценивается по величине рассеяния значений параметра Y вокруг условного среднего 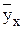. Большое рассеяние говорит о слабой зависимости Y от X, либо об ее отсутствии и, наоборот, малое рассеяние указывает на наличие достаточно сильной зависимости.

Коэффициент детерминации (по другому – детерминированности) показывает, на сколько процентов () найденная функция регрессии описывает связь между исходными значениями параметров X и Y

,

где 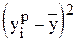– объясненная вариация; 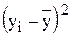– общая вариация.

Графическая интерпретация коэффициента детерминации

для случая линейной регрессии

Соответственно, величина показывает, сколько процентов вариации параметра Y обусловлены факторами, не включенными в регрессионную модель. При высоком (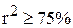) значении коэффициента детерминации можно делать прогноз для конкретного значения .

Дата добавления: 2014-01-05