Describe

Fit

Статистика

Подключение библиотеки осуществляется командой with(stats).
>with(stats);

Библиотека	Описание
importdata	импорт данных из файла
anova	вариационный анализ
describe	cтатистические данные
fit	аппроксимация
random	cлучайные значения
statevalf	численная оценка
statplots	графика
transform	преобразования данных

Рассмотрим функцию, предназначенную для нахождения корреляционных

отношений и для аппроксимации данных выбранными зависимостями с использованием метода наименьших квадратов.

fit[leastsquare[[x,y]]]([[dataX], [dataY]]);

По умолчанию система приближает зависимость к уравнению прямой линии
Пример
>fit[leastsquare[[x, y]]]([[10, 15, 17,19], [3, 4, 5, 6]]);

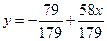
Можно самостоятельно задать вид уравнения, к которому необходимо приблизить зависимость.

Пусть наша зависимость выглядит следующим образом
>eq:=y=z*x^2+b*x+c;

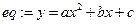
Тогда
>fit[leastsquare[[x, y], eq]]([[10, 15, 17,19], [3, 4, 5, 6]]);

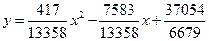
Решим задачу по отысканию вида функциональной зависимости, сформулированную нами для разбора подобного примера в электронных таблицах Excel.

Построим модель зависимости рентабельности работы предприятия (y) от удельного веса рабочих в структуре персонала (x₁), удельного веса покупных изделий (x₂), коэффициента сменности оборудования (x₃), среднегодовой численности персонала (x₄), среднегодовой стоимости основных производственных фондов (x₅). Предположим линейную функциональную зависимость вида

y= m₁x₁+ m₂x₂+ m₃x₃+ m₄x₄+ m₅x₅+b

В виде массивов введем данные:

удельный вес рабочих в структуре персонала (X₁);

удельный вес покупных изделий (X₂);

коэффициент сменности оборудования (X₃);

среднегодовая численность персонала (X₄);

среднегодовая стоимость основных производственных фондов (X₅);

рентабельность работы предприятия (Y).

> fit[leastsquare[[x1,x2,x3,x4,x5,y]]]([X1,X2,X3,X4,X5,Y]);

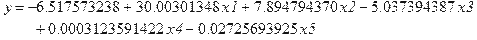
> evalf(%,5);

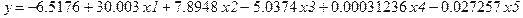
Коэффициенты, полученные в Maple и Excel, совпадают, что говорит о достоверности результатов и возможности использования любого из этих программных продуктов.

Эта библиотека позволяет вычислять широкий спектр описательных характеристик, используемых при анализе статистических данных.
Выделим некоторые наиболее употребляемые функции

Функция	Описание
coefficientofvariation	коэффициент вариации
сount	число элементов
сovariance	линейная ковариация
geometricmean	среднее геометрическое
linearcorrelation	линейная корреляция
mean	среднее арифметическое
median	медиана
quadraticmean	квадратичное среднее арифметическое
standarddeviation	стандартное отклонение
variance	дисперсия

Покажем на примере работу некоторых функций

>data1:=[1,2,3]:

>data2:=[3,5,7]:

>data3:=[7,5,3]:

>data4:=[1,2,3,4,5]:

>data5:=[0,5,-6,1,1]:

>describe[linearcorrelation](data1,data2);

>describe[linearcorrelation](data1,data3);

-1

>describe[linearcorrelation](data4,data5);

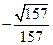
>evalf(%);

-0.07980868848

>describe[coefficientofvariation](data5);

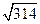
>describe[count](data5);

>describe[covariance](data4,data5);

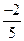
>describe[geometricmean](data1):evalf(%);

1.817120593

>describe[mean](data3):evalf(%);

5.

>describe[median](data4):evalf(%);

3.

>describe[quadraticmean](data4):evalf(%);

3.316624790

>describe[standartdeviation](data4):evalf(%);

1.414213562

>describe[variance](data4):evalf(%);

2.

Дата добавления: 2014-01-05