Ограниченные и монотонные

последовательности

Последовательность 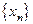называется ограниченной снизу, если существует вещественное число 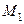, что все члены последовательности 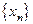удовлетворяют неравенству

.

Последовательность 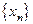называется ограниченной сверху, если существует вещественное число , что все члены последовательности 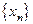удовлетворяют неравенству

.

Последовательность 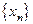называется ограниченной, если она ограничена и сверху и снизу, т.е. существуют вещественные числа 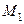и , что все члены последовательности 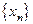удовлетворяют неравенству

.

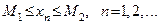Следующее определение является равносильным предыдущему определению.

Последовательность 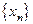называется ограниченной, если существует вещественное число 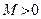, что все члены последовательности 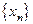удовлетворяют неравенству

.

Последовательность 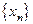называется неограниченной, если для любого вещественного числа 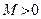найдется элемент 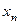последовательности 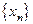, удовлетворяющий неравенству

.

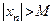Пример 3.1. Последовательность (пример 1.1.) является ограниченной снизу (найдите 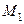), но не является ограниченной сверху.

Пример 3.2. Последовательность 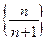(пример 1.2.) является ограниченной и снизу и сверху (найдите 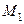и ).

Пример 3.3. Последовательность 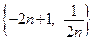(пример 1.3.) является ограниченной сверху (найдите ), но не является ограниченной снизу.

Пример 3.4. Последовательность 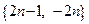(пример 1.4.) не является ограниченной снизу и сверху.

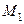Пример 3.5. Последовательность (пример 1.5.) является ограниченной и снизу и сверху (найдите и ).

Последовательность 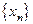называется монотонно возрастающей или неубывающей и обозначается 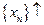, если каждый последующий член этой последовательности не меньше предыдущего:

или .

Последовательность 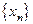называется монотонно убывающей или невозрастающей и обозначается 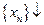, если каждый последующий член этой последовательности не больше предыдущего:

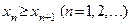или .

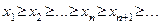Последовательность 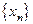называется строго монотонно возрастающей и обозначается , если каждый последующий член этой последовательности больше предыдущего:

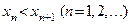или .

Последовательность 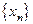называется строго монотонно убывающей и обозначается , если каждый последующий член этой последовательности меньше предыдущего:

или .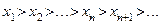

Дата добавления: 2014-01-05