Бесконечно малая величина

В теории числовых последовательностей важную роль играет бесконечно малая величина.

Последовательность 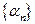называется бесконечно малой величиной, если она сходящаяся и её предел равен нулю:

.

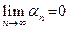Пример 5.1. Последовательность 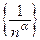, где 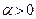– произвольное число, является бесконечно малой величиной:

.

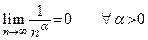Пример 5.2. Последовательность 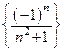–бесконечно малая величина:

.

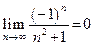Отметим два важных свойств бесконечно малых величин.

Свойство 5.1. Сумма двух бесконечно малых величин является бесконечно малой величиной.

Следствие 5.1. Сумма любого конечного числа бесконечно малых величин является бесконечно малой величиной.

Свойство 5.2. Произведение бесконечно малой величины на ограниченную величину является бесконечно малой величиной.

Связь между сходящейся последовательности, её пределом и бесконечно малой величины приводится в следующей теореме.

Теорема 5.1. Для того, что последовательность 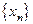являлась сходящейся с пределом равным 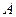, необходимо и достаточно, чтобы имело место представление

,

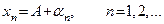где 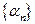– некоторая бесконечно малая величина.

Дата добавления: 2014-01-05