Линейные операторы

Определение. Отображение 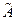линейного пространства в линейное пространство 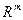называется линейным отображением (гомоморфизмом или морфизмом), если для любых элементов 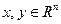и любого числа a справедливы равенства

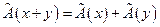, (33)

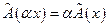(34)

Свойство (33) называется аддитивностью линейного отображения, а свойство (34) – однородностью этого отображения. В таком случае говорят, что задан линейный оператор 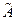, действующий из в .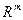

Будем говорить, что 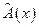является образом элемента .

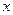Определение. Линейное отображение пространства в себя (т.е. когда пространства и 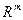совпадают) называется линейным оператором на линейном пространстве .

Пусть 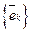- некоторый базис в векторном пространстве . Тогда разложение произвольного вектора 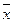по этому базису имеет вид:

.

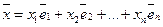Применим линейный оператор к вектору 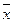. В силу свойств линейности (33) и (34) получаем:

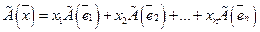(35)

Поскольку также является вектором из , его можно разложить по базису 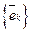. Пусть

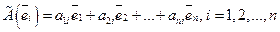(36)

Подставляя формулы (36) в (35), получаем:

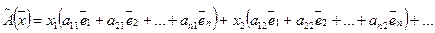
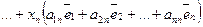
Группируя коэффициенты при базисных векторах 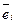, получаем:

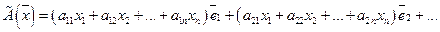
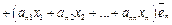(37)

Пусть вектор 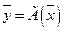имеет в том же базисе разложение

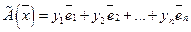(38)

Тогда в силу единственности разложения вектора в данном базисе получаем путем приравнивания коэффициентов при базисных векторах в разложениях (36) и (37):

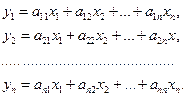(39)

Матрица 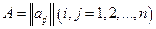, составленная из коэффициентов при 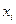, называется матрицей оператора 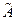в базисе 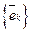. При этом ранг матрицы называется рангом оператора 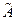. Как следует из формул (39), связь между вектором 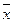и его образом можно выразить в матричной форме:

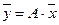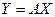или (40)

где , .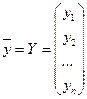

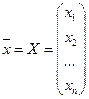Таким образом, каждому линейному оператору 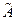в некотором базисе пространства соответствует матрица , по которой можно пересчитывать любой вектор в его образ в этом же базисе. Иными словами, любой линейный оператор можно задать в некотором базисе соответствующей матрицей.

Если матрицы является вырожденной, то оператор 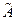называется вырожденным.

Пример. В пространстве 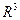линейный оператор 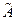задан в базисе 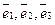матрицей

.

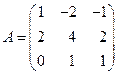Найти образ 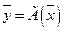вектора .

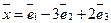Решение. По формуле (40) получаем

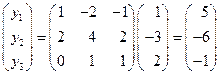
Таким образом, .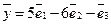

Для разных базисов матрицы одного и того же оператора будут разными. Связь между ними определяется теоремой.

Теорема. Пусть линейный оператор 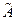задан матрицами и 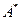соответственно в базисах 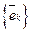и 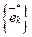. Тогда справедлива формула

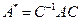(41)

где 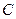- матрица перехода от базиса 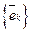к базису .

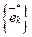Доказательство. Линейным оператором 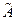вектор 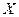пространства переводится в вектор 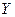этого же пространства, т.е. для обоих базисов справедливы равенства

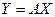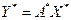, (42)

Поскольку 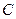- матрица перехода от базиса 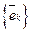к базису 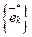, то имеем:

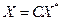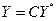, (43)

Умножив равенство 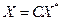слева на матрицу , получим

или с учетом равенства 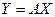, получим

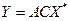
Подставляя выражение 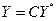, имеем

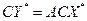
Умножая последнее равенство слева на матрицу 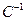, получаем окончательную формулу

.

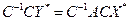
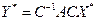Сравнивая последнее выражение с 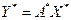(левые части равны, следовательно, равны и правые части):

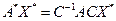
Умножим обе части равенства на справа, и учитывая, что 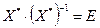, получаем:

,

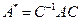получаем доказываемую связь между матрицами и .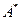

Пример. В пространстве 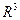линейный оператор 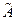задан в базисе 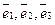матрицей

.

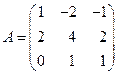Найти матрицу 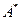оператора 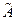в базисе , , .

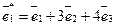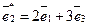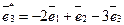Решение. Матрица перехода имеет вид

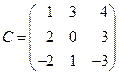, а обратная к ней матрица .

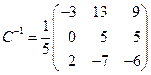Следовательно, по формуле (41) получаем:

.

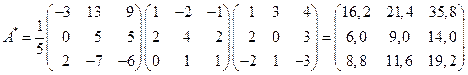Дата добавления: 2014-01-05