
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Свойства арифметических операций над комплексными числами
|
|
|
|
1.  При сложении (вычитании) комплексных чисел их радиусы-векторы складываются (вычитаются) по правилу параллелограмма.
При сложении (вычитании) комплексных чисел их радиусы-векторы складываются (вычитаются) по правилу параллелограмма.
2. Модуль произведения (частного) двух комплексных чисел равен произведению (частному) модулей этих чисел, а его аргумент – сумме (разности) аргументов этих чисел, т.е.,
если 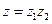 , то
, то 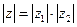 ,
, 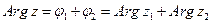 и
и
 , (93)
, (93)
если  , то
, то  ,
, 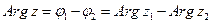 и
и
 (94)
(94)
Геометрически умножение числа  на число
на число  означает изменение длины радиуса-вектора
означает изменение длины радиуса-вектора 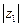 (или
(или  ) в
) в 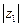 (или
(или 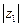 ) раз и его поворот вокруг точки О против часовой стрелки на угол
) раз и его поворот вокруг точки О против часовой стрелки на угол  (или
(или  ).
).
Так как в соответствии с формулами (93) и (94) при умножении комплексных чисел их модули перемножаются, а аргументы складываются, то формула Муавра - возведения комплексного числа в натуральную степень 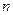 , имеет вид:
, имеет вид:
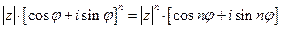 (95)
(95)
Пример. Комплексные числа  и
и 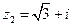 представить в тригонометрической форме и найти
представить в тригонометрической форме и найти 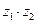 и
и  .
.
Решение.
1. Запишем тригонометрическую форму комплексного числа  , используя формулу (92):
, используя формулу (92):  , т.к.
, т.к. 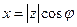 , то
, то 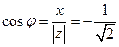 , т.к.
, т.к.  , то
, то 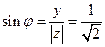 , тогда
, тогда 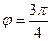 , т.е.
, т.е. 
2. Выполним аналогичные действия для комплексного числа  :
:  , т.к.
, т.к. 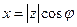 , то
, то  , т.к.
, т.к.  , то
, то 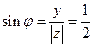 , тогда
, тогда 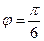 , т.е.
, т.е.  .
.
3. Применяя формулы (93) и (94), получаем:
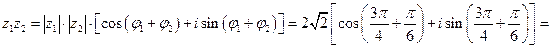
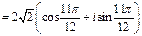
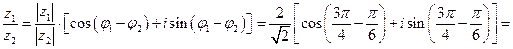
 .
.
Пример. Найти 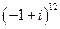 .
.
Решение.
В примере, решенном ранее, была получена тригонометрическая форма для комплексного числа 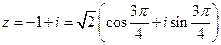 . Поэтому по формуле Муавра находим:
. Поэтому по формуле Муавра находим:
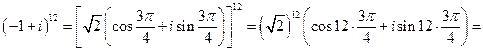
 .
.
Рассмотрим извлечение корня из комплексного числа. Пусть

Тогда, используя определение корня и формулу Муавра, получаем
 или
или

Откуда следует, что
 и
и 
Итак,  ,
,  , т.е.
, т.е.
 , (96)
, (96)
где  .
.
При 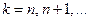 значения корня будут повторяться. Таким образом, корень
значения корня будут повторяться. Таким образом, корень 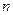 -й степени из комплексного числа (не равного нулю) имеет
-й степени из комплексного числа (не равного нулю) имеет 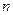 различных значений.
различных значений.
Пример. Найти 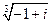 .
.
Решение.
В примере, решенном ранее, была получена тригонометрическая форма для комплексного числа 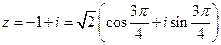 . Поэтому по формуле (96) имеем:
. Поэтому по формуле (96) имеем:
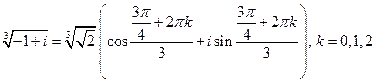 .
.
откуда получаем три значения корня
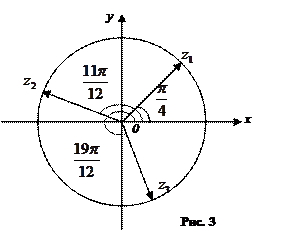

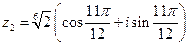
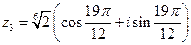
На комплексной плоскости найденные значения корня представляют равноотстоящие друг от друга точки  , расположенные на окружности радиуса
, расположенные на окружности радиуса 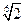 .
.
Связь между тригонометрическими и показательными функциями выражается формулой Эйлера:
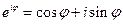 (97)
(97)
тогда показательная форма комплексного числа имеет вид:
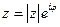 (98)
(98)
Пример. Комплексные числа  и
и 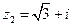 представить в показательной форме.
представить в показательной форме.
Решение.
Ранее было получено
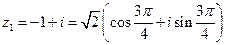 ,
, 
Следовательно, по формуле (98) получим:
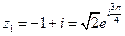 ,
, 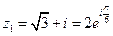 .
.
Оглавление
| Тема 1. Матрицы. Определители. | |
| 1.1. Матрицы. | |
| 1.2. Операции над матрицами. | |
| 1.3. Определители квадратных матриц. | |
| 1.4. Свойства определителей. | |
| Тема 2. Обратная матрица. Ранг матрицы. | |
| 2.1. Обратная матрица. | |
| 2.2. Ранг матрицы. | |
| Тема 3. Системы линейных алгебраических уравнений. | |
| 3.1.Общий вид и свойства системы уравнений. | |
| 3.2. Матричная форма системы уравнений. | |
| 3.3. Метод обратной матрицы и метод Крамера. | |
| 3.4. Метод Гаусса. | |
3.5. Система  линейных уравнений с линейных уравнений с 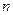 неизвестными. неизвестными.
| |
| 3.6. Системы линейных однородных уравнений. Фундаментальная система решений. | |
| 3.7. Модель Леонтьева многоотраслевой экономики. | |
| Тема 4. Векторы. | |
| 4. 1. Векторы на плоскости и в пространстве. | |
| 4.1.1. Скаляры и векторы. Операции над векторами. | |
| 4.1.2. Скалярное произведение векторов. | |
| 4.2. Векторное пространство. | |
| 4.2.1. Понятие и основные свойства векторов. | |
| 4.2.2. Операции над векторами. | |
| 4.2.3. Скалярное произведение векторов. | |
| 4.3. Линейная зависимость векторов. | |
| 4.3.1. Линейно зависимые и линейно независимые системы векторов. | |
| 4.3.2. Базис и ранг системы векторов. | |
| 4.4. Разложение вектора по базису. | |
| 4.4.1. Представление вектора в произвольном базисе. | |
| 4.4.2. Разложение вектора в ортогональном базисе. | |
| 4.5. Оператор линейного преобразования. | |
| 4.5.1. Матрица перехода от одного базиса к другому. | |
| 4.5.2. Линейные операторы. | |
| 4.5.3. Собственные значения и собственные векторы матрицы. | |
| 4.5.4. Собственные значения и собственные векторы линейного оператора. | |
| 4.5.5. Диагональная форма матрицы оператора. | |
| 4.6. Квадратичные формы. | |
| 4.6.1. Основные сведения о квадратичных формах | |
| 4.6.2. Преобразование квадратичных форм. | |
| 4.6.3. Канонический и нормальный виды квадратичной формы. | |
| 4.6.4. Критерий знакоопределенности квадратичной формы. | |
| 4.6.5. Линейная модель торговли. | |
| Тема 5. Аналитическая геометрия на плоскости. | |
| 5.1. Уравнение линии на плоскости. | |
| 5.1.1. Линии первого порядка. | |
| 5.2. Линии второго порядка. | |
| 5.2.1. Эллипс. | |
| 5.2.2. Гипербола. | |
| 5.2.3. Парабола. | |
| Тема 6. Аналитическая геометрия в пространстве. | |
| 6.1. Плоскость в пространстве. | |
| 6.2. Прямая в пространстве. | |
| 6.3. Взаимное расположение прямой и плоскости. | |
| 6.4. Поверхности второго порядка. | |
| Тема 7. Комплексные числа. | |
| 7.1. Арифметические операции над комплексными числами. | |
| 7.2. Тригонометрическая и показательная формы комплексного числа. | |
| Литература |
Литература
1. Кремер Н.Ш. Высшая математика для экономических специальностей: учебник и практикум / Н.Ш. Кремер, Б.А. Путко, И.М. Тришин, М.Н. Фридман: под ред. Н.Ш. Кремера. – 3-е изд.. – М.: Издательство Юрайт; ИД Юрайт, 2012. – 909 с.
2. Шипачев В.С. Высшая математика. Учебник.- М.: Высшая школа, 2003.-479 с.
3. Красс М.С. Математика для экономических специальностей. Учебник. - М.: ИНФРА-М, 1998. – 464 с.
4. Шипачев В.С. Задачник по высшей математике. Учебное пособие для вузов. - М.: Высшая школа, 2003.- 304 c.
5. Минорский В.П. Сборник задач по высшей математике: Учеб. Пособие для втузов.- 14-е изд., испр. - М.: Издательство Физико-математической литературы, 2001. – 336 с.
6. Солодовников А.С., Бабайцев В.А., Браилов А.В. Математика в экономике: учебник. - ч. 1. – М.: Финансы и статистика, 2000. – 224 с.
|
|
|
|
Дата добавления: 2014-01-05; Просмотров: 660; Нарушение авторских прав?; Мы поможем в написании вашей работы!