Свойства простых чисел

1. Для " n Î N и любого простого p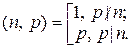

2. (p ₁, p ₂) = 1, если p ₁ ¹ p ₂ – различные простые числа.

Заметим, что из соотношения 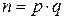натуральных чисел при n > 1, 1 < p, q < n следует, что либо 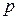, либо 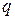принадлежит отрезку [2; 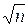]. Истори-чески первый метод проверки числа n на простоту заключался в делении его на простые числа, не превосходящие 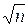. Если среди таких чисел делителей не найдено, то n – простое число. Это один из вариантов так называемого «реше-та» Эратосфена, ставшего его наиболее знаменитым достижением. Эратосфен (ок. 276–194 до н. э.) – один из самых разносторонних ученых Античности.

2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12,…, [],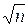

где [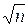] – целая часть :

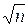1) 2 – простое число, исключаем все числа, кратные 2 (2 | n – да или нет?);

2) 3 – простое число, исключаем все числа, кратные 3 (3 | n – да или нет?);

и т. д. до ближайшего к 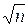простого числа.

В целом «решето» Эратосфена решает более общую задачу нахождения всех простых чисел на отрезке натурального ряда [ m; n ], где m < n.

Теорема 1.3.2 (Евклид). Простых чисел бесконечно много.

Пусть p ₁, p ₂,…, p_k, k Î N, – все простые числа. Рассмотрим число N = p ₁ × p ₂ ×…× p_k + 1. N не делится ни на одно из p_i, 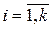, т. к. в противном случае для некоторого i p_i | 1 (свойство делимости целых чисел 6), что невозможно. Поэтому N является либо новым простым числом, либо составным, в последнем случае существует отличное от всех p_i простое число p, где p | N.

Значение простых чисел в том, что они, согласно теореме 1.3.1, являются составными «кирпичиками» всех натуральных чисел. Распределение простых чисел среди натуральных весьма непредсказуемо, о чем свидетельствуют следующие две теоремы. Теорема 1.3.3, доказанная в 1852 г. выдающимся русским математиком и механиком Пафнутием Львовичем Чебышевым (1821–1894), приводится здесь без доказательства.

Теорема 1.3.3 (П. Л. Чебышев). Между натуральными числами k и 2 k, k > 1, обязательно найдутся простые.

Теорема 1.3.4. Для всякого натурального n существует отрезок 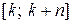, k Î N, натурального ряда, все числа которого составные.

В самом деле, все следующие числа составные:

k = (n + 2)! + 2,…, k + n = (n + 2)! + 2 + n.

Действительно, k = 2 × (3 ×…× (n + 2) + 1),…, k + n = (n + 2) × (2 ×…× (n + 1) + 1) (здесь m! = 1 × 2 × 3 ×…× k для m Î N, 0! = 1).

Несмотря на теорему 1.3.4, для x Î N _>2 количество p(x) всех простых чисел, меньших x, подчинено достаточно равномерному закону.

Дата добавления: 2014-01-05