
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Три формы представления уравнения Бернулли для потока реальной жидкости
Дифференциальное уравнение движения невязкой жидкости (уравнение Эйлера)
Предположим, что в жидкости движется элементарный объем в форме параллелепипеда со сторонами dx, dy, dz (см. рис. 2.38). На параллелепипед действуют поверхностные силы давления и массовые силы с проекциями X, Y, Z, отнесенными к единице массы. При движении объема возникают силы инерции. Проекции этих сил на оси координат, отнесенные к единице массы, равны соответственно: 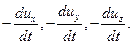
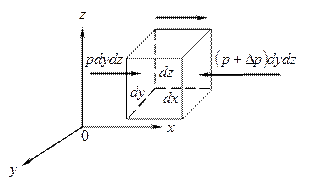
Рис. 2.38. Схема равномерного движения объема жидкости
Рассмотрим условие равновесия сил, в проекции на ось х. Сила давления на левую грань – pdydz, на правую грань
– (p +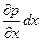 ) dydz,
) dydz,
где 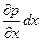 =Δ p – изменение давления вдоль оси x.
=Δ p – изменение давления вдоль оси x.
Массовая сила равна X ρ dxdydz. Уравнение равновесия запишется в виде
pdydz – (p +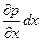 ) dydz + X ρ dxdydz
) dydz + X ρ dxdydz 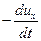 ρ dxdydz = 0,
ρ dxdydz = 0,
или
– 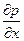 dxdydz + X ρ dxdydz
dxdydz + X ρ dxdydz ρ dxdydz = 0.
ρ dxdydz = 0.
Разделив каждый член уравнения на ρdxdydz, получим
X – 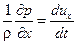 .
.
Соответственно для осей и уравнение равновесия будет выглядеть следующим образом
Y – 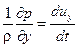 ,
,
Z – 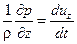 .
.
Объединив полученные уравнения, получим систему уравнений Эйлера:
X – 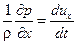 ,
,
Y – 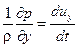 , ,
| (2.42) |
Z – 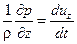 .
.
Можно получить полный дифференциал уравнений Эйлера для установившегося движения, если рассматривать перемещение частиц жидкости вдоль линии тока. Для этого надо умножить каждое из уравнений системы на соответствующую проекцию элементарного перемещения частиц dx, dy, dz, и сложить их:
(Xdx + Ydy + Zdz) – 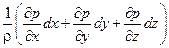 –
– 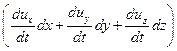 = 0.
= 0.
Т.к. для установившегося течения линии тока совпадают с траекториями движения частиц, то
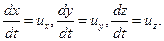
Тогда
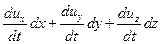 =
= 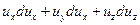 =
= 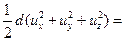
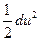
Для установившегося движения давление зависит только от координат, поэтому второй член уравнения есть полный дифференциал давления dp. Получим
(Xdx + Ydy + Zdz) – 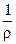 dp – dp – 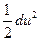 = 0 = 0
| (2.43) |
Мы получили дифференциальное уравнение движения невязкой жидкости.
В поле силы тяжести
X = 0, Y = 0, Z = – g,
тогда уравнение запишется в следующем виде
– gdz – 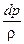 –
– 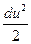 = 0.
= 0.
После интегрирования этого уравнения получаем (при ρ = const) уравнение
gz + 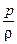 + + 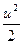 = const, = const,
| (2.44) |
которое называется уравнением Бернулли для струйки невязкой жидкости.
2.2.6. Общее уравнение энергии в интегральной форме
(Уравнение Бернулли для потока реальной жидкости)
Для двух сечений струйки невязкой жидкости это уравнение будет выглядеть следующим образом
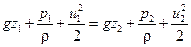 . .
| (2.45) |
Сумма слева представляет полную удельную энергию струйки в сечении 1-1, сумма справа – полную удельную энергию струйки в сечении 2-2. Можно записать, что
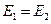 .
.
На практике энергия струйки в начале больше энергии струйки в конце, т.к. часть энергии теряется на преодолении сил вязкости. В процессе движения вязкой жидкости запас ее механической энергии уменьшается, и на самом деле
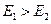 .
.
Обозначим энергию, затрачиваемую на преодоление сил сопротивления Eпот. Eпот – это та часть механической энергии, которая, вследствие вязкости, переходит в тепловую энергию. Другими словами можно сказать, что Eпот – это часть энергии, которая израсходована на преодоление гидравлических сопротивлений.
| Е 1 = Е 2 + Eпот. | (2.46) |
При выводе уравнения Бернулли для элементарной струйки можно было пренебречь изменением скорости и давления в пределах нормальных сечений благодаря их малым величинам. В потоке жидкости скорости и давления в пределах живых сечений различны, и это необходимо учитывать. Согласно гипотезе Ньютона, жидкость как бы прилипает к стенкам канала, по которому она течет и ее скорость равна нулю. Но с увеличением расстояния от стенки, скорость струек увеличивается. Так называемая мощность потока складывается из энергии отдельных струек
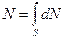 ,
,
где N – мощность потока; dN – мощность струйки; S – площадь живого сечения потока.
Для мощности струйки можно записать:
dN = Ed 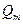 = (gz +
= (gz + 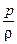 +
+ 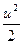 ) ρ uds,
) ρ uds,
где ds – площадь живого сечения струйки.
Величина удельной энергии потока равна частному от деления мощности потока на массовый расход 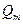
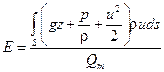 .
.
Это уравнение можно разбить на два интеграла
E =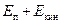 =
=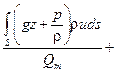
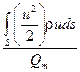 ,
,
где 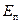 – удельная потенциальная энергия потока относительно выбранной плоскости сравнения;
– удельная потенциальная энергия потока относительно выбранной плоскости сравнения;  – удельная кинетическая энергия потока.
– удельная кинетическая энергия потока.
Для вычисления 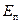 надо знать закон изменения давления по живому сечению. Для плавноизменяющихся течений ускорения и силы инерции незначительны, поэтому ими можно пренебречь. Экспериментально доказано, что в плавноизменяющемся потоке давления распределяются по закону гидростатистики gz
надо знать закон изменения давления по живому сечению. Для плавноизменяющихся течений ускорения и силы инерции незначительны, поэтому ими можно пренебречь. Экспериментально доказано, что в плавноизменяющемся потоке давления распределяются по закону гидростатистики gz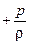 = const.
= const.
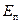 = =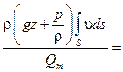 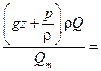 gz gz 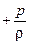 . .
| (2.47) |
Для вычисления интеграла 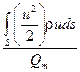 нужно знать закон распределения скоростей по сечению. Умножим и поделим это выражение на
нужно знать закон распределения скоростей по сечению. Умножим и поделим это выражение на 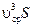 .
.
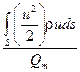
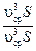 =
=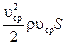
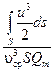 =
=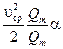 ,
,
где α – коэффициент, который учитывает неравномерность распределения скоростей в сечении, называется коэффициент Кориолиса. Получаем выражение для удельной кинетической энергии потока:
 = =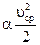 . .
| (2.48) |
Запишем уравнение Бернулли для двух сечений потока реальной жидкости
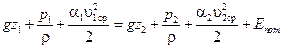 . .
| (2.49) |
Полученное уравнение позволяет сделать следующие выводы:
1. При увеличении кинетической энергии потока от одного сечения к другому потенциальная энергия уменьшается, и, наоборот, с увеличением потенциальной энергии, кинетическая уменьшается.
2. Коэффициент α тем больше, чем больше скорости отдельных струек отличаются от величины средней скорости. Если скорости всех элементарных струек будут равны средней скорости, то α = 1.
Представленное выше уравнение Бернулли является уравнением Бернулли, записанное в форме удельной энергии, где:
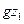 и
и 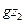 – удельная энергия положения в сечениях 1-1 и 2-2 потока;
– удельная энергия положения в сечениях 1-1 и 2-2 потока;
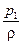 и
и 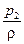 – удельная энергия давления в этих сечениях;
– удельная энергия давления в этих сечениях;
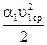 и
и 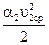 – удельная кинетическая энергия.
– удельная кинетическая энергия.
На практике при выполнении инженерных расчетов обычно применяют две другие формы представления уравнения Бернулли.
Уравнение Бернулли в форме напоров можно получить, если разделить уравнение в форме удельной энергии на g, обозначив 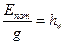 .
.
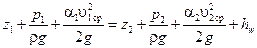 . .
| (2.50) |
Каждый член этого выражения имеет размерность длины и может быть представлен некоторой высотой (напором) (см. рис. 2.39).
Здесь 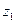 и
и 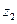 – высота положения или геометрический напор (расстояние от плоскости сравнения до центра сечения потока);
– высота положения или геометрический напор (расстояние от плоскости сравнения до центра сечения потока);
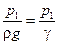 и
и 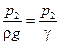 – пьезометрическая высота или пьезометрический напор (высота поднятия жидкости в пьезометрической трубке под действием давления);
– пьезометрическая высота или пьезометрический напор (высота поднятия жидкости в пьезометрической трубке под действием давления);
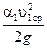 и
и 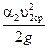 – скоростной напор (разность показаний трубки Пито и пьезометрической трубки).
– скоростной напор (разность показаний трубки Пито и пьезометрической трубки).
Сумма трех высот 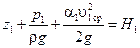 и
и 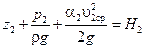 – полный напор потока жидкости.
– полный напор потока жидкости.
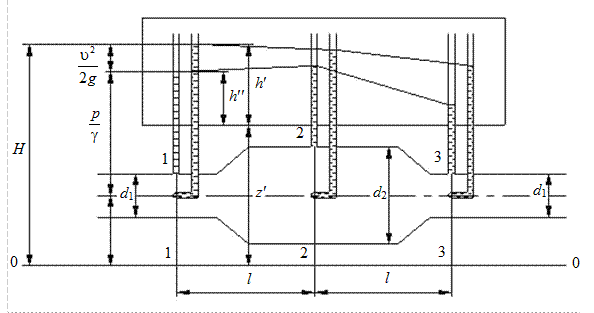
Рис. 2.39. Опытная демонстрация уравнения Бернулли в форме напоров
Разность полных напоров двух живых сечений потока – потеря напора между этими сечениями
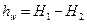 . .
| (2.51) |
С помощью уравнения Бернулли в форме напоров можно найти высотные отметки жидкостей, которые могут быть достигнуты в данной трубопроводной системе. Это уравнение широко используется при проектировании и гидравлических расчетах водопроводов.
Уравнение Бернулли в форме давлений получаем, если уравнение Бернулли в форме удельной энергии умножим на плотность ρ.
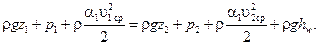
| (2.52) |
Здесь каждый член имеет размерность давления:
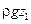 и
и 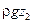 – гравитационное давление, т. е. давление, создаваемое силой тяжести;
– гравитационное давление, т. е. давление, создаваемое силой тяжести;
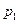 и
и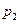 – статическое давление;
– статическое давление;
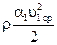 и
и 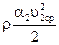 – динамическое давление;
– динамическое давление;
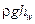 – потери давления на преодоление сил трения и местные сопротивления.
– потери давления на преодоление сил трения и местные сопротивления.
Вывод: при увеличении скорости движения потока давление на этом участке падает и, наоборот – при уменьшении скорости давление увеличивается.
Уравнение Бернулли в форме давлений применяется для расчета систем вентиляции, газовых стояков внутри зданий и т.д.
|
Дата добавления: 2014-01-05; Просмотров: 1902; Нарушение авторских прав?; Мы поможем в написании вашей работы!