Истечение жидкостей из отверстия в тонкой стенке

При истечении жидкости из какого-либо резервуара происходит процесс превращения запаса потенциальной энергии в кинетическую энергию свободной струи. Основной вопрос исследования – определение скорости истечения и расхода жидкости для различных форм отверстий и насадков.

Рассмотрим истечение жидкости через круглое отверстие в тонкой стенке (рис. 4.20). Отверстием в тонкой стенке называется отверстие, толщина стенок которого составляет не более 1/4 диаметра. Рассмотрим случай, когда жидкость вытекает из резервуара в атмосферу (см. рис. 4.20). Напишем уравнение энергии в форме напоров для сечения 1-1 и С - С. Обозначим давление на поверхности жидкости в резервуаре p ₀, 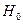– заглубление центра отверстия под уровнем жидкости в сосуде. Струя, вытекающая под давлением столба жидкости высотой 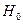и разностью давлений , при выходе из отверстия сжимается до сечения С-С. В сечении С-С струйки приблизительно параллельны и движение можно считать плавноизменяющимся, поэтому для этого сечения можно применить уравнение Бернулли. Такое сжатие обуславливается инерцией частиц жидкости, движущихся при подходе к отверстию по криволинейным траекториям. Степень сжатия струи оценивается коэффициентом

,

(4.21)

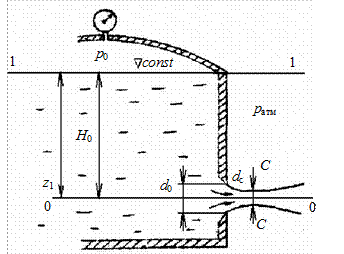
Рис. 4.20. Истечение жидкости из отверстия в тонкой стенке

где 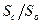– отношение площади струи в сжатом сечении к площади отверстия.

Для плоскости сравнения, проведенной относительно оси отверстия, запишем уравнение Бернулли для движения жидкости от свободной поверхности, где скорость можно принять равной нулю, до сечения С - С

,

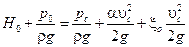где – коэффициент сопротивления отверстия.

Выполним небольшие преобразования

или ,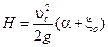

где H – расчетный напор

.

(4.22)

Скорость истечения

,

(4.23)

где φ – коэффициент скорости.

Нами получена формула Торричелли для определения скорости струи, вытекающей из резервуара.

Если резервуар открыт, то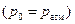, тогда

и .

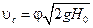(4.24)

Расход через сжатое сечение

,

где ε – коэффициент сжатия струи; 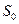– площадь сечения отверстия.

Окончательно получаем:

,

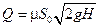(4.25)

где μ – коэффициент расхода.

4.10. Зависимость коэффициентов истечения
от числа Рейнольдса

При истечении вязких жидкостей (например, дизельного топлива через форсунки) или при истечении с небольшими скоростями маловязких жидкостей (при малых числах Рейнольдса) будет проявляться зависимость величин коэффициентов истечения μ, φ, ε от Re (см. рис. 4.21).

Рис. 4.21. Зависимость коэффициентов истечения от числа Рейнольдса

При истечении через малое отверстие в тонкой стенке коэффициент скорости φ с увеличением Re возрастает, что связано с уменьшение сил вязкости, что в свою очередь сказывается на уменьшении коэффициента сопротивления ξ. Коэффициент сжатия уменьшается вследствие увеличения радиусов кривизны поверхности струи на её участке от кромки до сжатого сечения С-С (см. рис. 4.22). При Re → ∞ значения коэффициентов φ и ε приближаются к значениям, соответствующим истечению идеальной жидкости (φ = 1, ε = 0,6).

Рис. 4.22. Истечение жидкости из отверстия

Изменение величины коэффициента расхода μ определяется его зависимостью от коэффициентов φ и ε:

.

(4.26)

Зная характер изменения коэффициентов μ, φ, ε от числа Re при истечении через отверстия и насадки, можно с большей точностью определить скорость 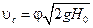, расход Q и другие параметры потока.

При больших числах Re (турбулентный режим) коэффициенты истечения постоянны, зависят только от вида отверстия, определяются опытным путем и приводятся в справочниках.

Дата добавления: 2014-01-05