Несобственные интегралы

Эпизод 4. Закат Киевской Руси.

Эпизод 4. Русское летописание

Эпизод 3. Владимир Мономах

Эпизод 2. Недружные Ярославичи

Лекция 2. Расцвет Киевской Руси

Эпизод 1. Ярослав Мудрый (1016-1054 гг.)

- борьба Ярослава со Святополком Окаянным, битва при Альме, паралич.

- борьба с Мстиславом Удалым, Тмутаракань,

- строительство г. Ярославль, Юрьев (Тарту),

- Софийский собор 1037 г., византийские мозаики, «Нерушимое Стено» – Богородица Оранта,

- книгочей, первая библиотека при соборе,

- первый митрополит Илларион («благ, книжен и постник») основание Киево-Печерского монастыря, 1051 г.

- «Русская правда» - закон Русский (обычая Руси), «Божий суд» -- испытание огнем, отмена кровной мести.

- семейные связи: жена Ярослава Ингигерда, дочь шведского короля Олафа, сын Всеволод женат на дочери византийского императора Константина Мономаха, дочь Анна Ярославна замужем за французским королем Генрихом Первым, регентша Франции с 1049 г.,

- «Правда Ярославичей», дополнение к «Русской правде»,

- фактор Степи. Приход половцев (тюрки), которые изгнали печенегов, первый крестовый поход 1111 г.,

- Любечский съезд Ярославичей 1097 г., персидский ковер – нейтральное поле,

- Олег Святославич – «Гориславич».

- личность князя, 1113 г.

- «Поучение Владимира Мономаха», «Человек погибает внезапно», «Погоди, татарин. Дай саблю выну»

- Моравский князь – византийскому императору: «Земля наша крещена, но нет в ней учителя»; Кирилл (Констатин) – кириллица на основе греческого алфавита, вторая половина 9 века. Мефодий – перевод Евангелия, использования славянского языка при богослужении.

- летописи при Ярославе, 1037 г., скрипторий при Св.Софии, летописный свод-склейка,

- Нестор-летописец, 1113 г. «Книги – реки, которые питают вселенную», «Повесть временных лет», нетленная правая рука.

- смерть Владимира Мономаха, 1125 г., распри Мономаховичей

- причины упадка: усиление внутренней славянской колонизации, опасность степи, развитие региональных центров, значение местных династий, рыхлость государственности, престолонаследование.

Константин Мирошник и Наталия Кургузова-Мирошник Владимир Мономах

А. Кившенко. Долобский съезд князей.

Свидание Владимира Мономаха с князем Святополком. 1103 год

Васнецов. Святополк Окаянный

А.Жабский. На половецкие степи

Пусть функция f (x) определена на полуинтервале (a, b ] и 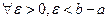, 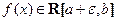; кроме того

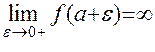
Определение: Несобственным интегралом 1рода от f (x) на (a, b ] называется предел:

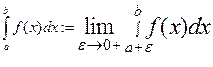
если этот предел существует. В этом случае говорят, что несобственный интеграл сходится.

Пример:

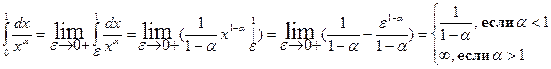
Если a = 1, то

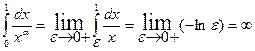
Следовательно, при a < 1 интеграл

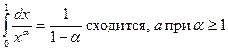
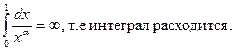
Аналогично определяется несобственный интеграл, если

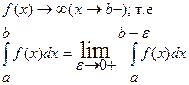
Определение несобственного интеграла 2 рода:

Пусть 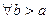: 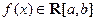и существует предел:

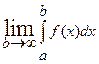
Тогда этот предел называется несобственным интегралом 2 рода, т.е.

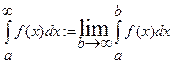
Пример:

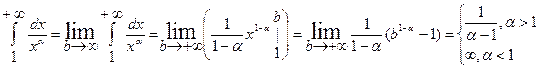
Если a = 1, то

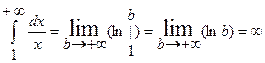
Следовательно, несобственный интеграл

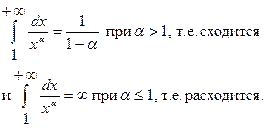
Для исследования сходимости и расходимости несобственных интегралов применяется признак сравнения:

Пусть функция f (x) и g (x) удовлетворяют неравенству: 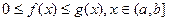и несобственный интеграл 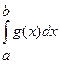сходится. Тогда сходится и несобственный интеграл .

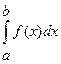Доказательство: В силу сходимости 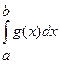по критерию Коши для функции 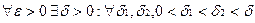, выполняется неравенство 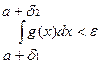. Но тогда, ввиду неравенств: 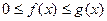аналогично неравенство будет справедливо и для функции f (x), т.е.

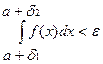
Следовательно, по критерию Коши существует предел:

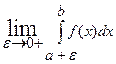, т.е. этот интеграл сходится.

Замечание1: Аналогичный признак сравнения справедлив и для несобственных интегралов 2 рода.

Замечание2: Отрицанием признака сравнения будет следующее утверждение: если несобственный интеграл 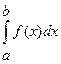расходится, то расходится и несобственный интеграл .

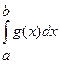Эйлеровы интегралы G(a) и B(a, b).

Определим функцию G(a) равенством:

.

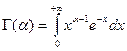Покажем, что интеграл сходится при a > 0. Представим этот интеграл в виде суммы двух интегралов:

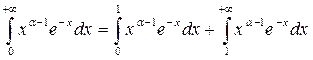
и докажем сходимость каждого из этих интегралов при a > 0.

Обозначим 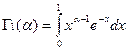и .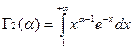

Если x Î(0, 1], то: 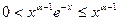. Так как интеграл 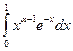, как это было доказано выше сходится при 1 - a< 1, т.е. при a>0, то по признаку сравнения интеграл 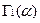сходится при a>0. Если x Î[1, + ), то для некоторой константы c >0 выполняется неравенство: .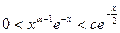

Заметим, что 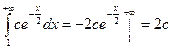, т.е. этот интеграл сходится при любых aÎ R. Следовательно, функция Эйлера G(a) = G₁(a) + G₂(a) определена для всех a>0.

Далее, определим функцию B(a, b) = 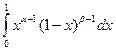и докажем, что эта функция определена для любых a>0 и b>0.

Обозначим: 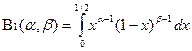и .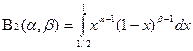

Если x Î(0, 1/2], то 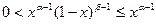. Интеграл 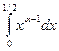сходится по признаку сравнения 1 - a<1, т.е. при a>0 и при любых значениях b. Заметим, что, если в интеграле B₂(a, b) сделать замену t = 1 – x, то мы B₁(b, a), который, как мы выяснили, сходится при b>0 и при любых a.

Следовательно, функция Эйлера B(a, b) = B₁(a, b) + B₂(a, b) определена для любых a>0 и b>0. Отметим (без доказательства) следующие свойства интегралов Эйлера:

1) G(1) = 1

2) G(a + 1) = aG(a), a>0

3) G(n + 1) = n!, nÎ N

4) G(a)G(1 - a) =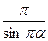, 0<a<1

5) G(1/2) =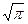

6) B(a, b) =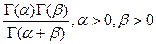

Пример:

Вычислить интеграл вероятности .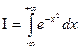

В силу чётности функции 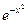интеграл вероятности можно представить в виде:

.

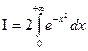Сделав в этом интеграле замену t = x², получим следующий интеграл:

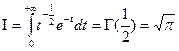
Дата добавления: 2014-01-05