Сферические координаты в трехмерном пространстве

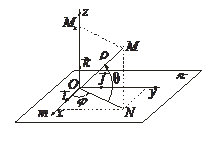Помимо уже известных систем координат для определения положения точки в трехмерном пространстве используют сферическую систему координат.

Для ее определения зафиксируем в некоторой плоскости p точку О — полюс и через нее в плоскости p проведем луч Оm с началом в точке О. Пусть ось 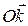с направляющим вектором 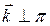(рис. 3.14.1).

Пусть М — некоторая точка пространства и N — ее ортогональная проекция на плоскость p; 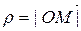— сферический радиус, r Î [0, +¥). Угол 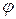, на который следует повернуть против часовой стрелки, если смотреть со стороны положительного направления вектора 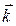, луч Оm до совмещения его с лучом ON, называется долготой, 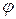= Ð(Оm, ON), 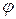Î [0, 180^°). Угол между лучом ОМ и его проекцией ON, называется широтой q, причем q = Ð(ON, OM), q Î [– 90^°, 90^°].

Упорядоченная тройка чисел (r, 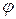, q), взятая именно в таком порядке, называется сферическими координатами точки М, при этом используется обозначение М (r, 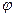, q).

Между всевозможными точками трехмерного пространства и упорядоченными тройками чисел (r, 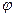, q), где r Î [0, +¥), 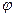Î [0, 180^°), q Î [– 90^°, 90^°] сферическая система координат устанавливает взаимно однозначное соответствие.

Подчеркнем, что для полюса r = 0, а долгота 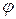и широта q считаются не определенными.

Пусть сферическая и декартовая системы координат связаны следующим образом: они имеют общее начало О, общую 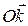ось , ось 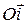направлена по лучу Om, ось 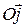выбрана так, чтобы тройка векторов 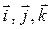была правой. Тогда сферические и декартовые координаты одной и той же точки М трехмерного пространства связаны соотношениями

x = r cos q cos j, y = r cos q sin j, z = r sin q.

Иногда в качестве широты q рассматривают угол между осью 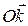и лучом ОМ, q = Ð(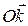, OM), 0 £ q £ 180^°. В этом случае связь между сферическими и декартовыми координатами одной и той же точки выражается соотношениями

x = r sin q cos j, y = r sin q sin j, z = r cos q.

Дата добавления: 2014-01-05