
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Обратная матрица
|
|
|
|
Определение 2.9.1. Правой обратной матрицей для матрицы  называется такая матрица
называется такая матрица 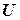 , что
, что  , где
, где  — единичная матрица.
— единичная матрица.
Определение 2.9.2. Левой обратной матрицей для матрицы  называется такая матрица
называется такая матрица  , что
, что 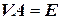 , где
, где  — единичная матрица.
— единичная матрица.
Определение 2.9.3. Матрица  называется невырожденной, если
называется невырожденной, если 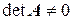 , в противном случае, она называется вырожденной.
, в противном случае, она называется вырожденной.
Определение 2.9.4. Матрица 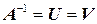 , одновременно являющаяся как правой, так и левой обратной матрицей, называется обратной матрицей для матрицы
, одновременно являющаяся как правой, так и левой обратной матрицей, называется обратной матрицей для матрицы  .
.
Теорема 2.9.1. Матрица 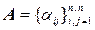 имеет обратную матрицу тогда и только тогда, когда она невырожденная.
имеет обратную матрицу тогда и только тогда, когда она невырожденная.
Доказательство. Необходимость. Пусть
 .
.
Достаточность. Пусть 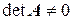 . Построим вспомогательную матрицу
. Построим вспомогательную матрицу 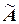 , состоящую из алгебраических дополнений элементов матрицы
, состоящую из алгебраических дополнений элементов матрицы 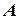 , следующим образом:
, следующим образом:
 .
.
Произведение

 . (2.9.1)
. (2.9.1)
В соответствии с теоремой о разложении определителя по элементам какой-либо строки имеем
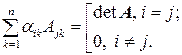 (2.9.2)
(2.9.2)
Следовательно, произведение
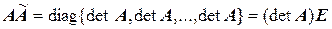 ,
,
поэтому матрица 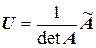 является правой обратной матрицей.
является правой обратной матрицей.
Аналогично показывается, что 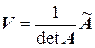 является левой обратной матрицей. Таким образом, по определению обратная матрица
является левой обратной матрицей. Таким образом, по определению обратная матрица
 .
.
Определение 2.9.5. Матрица 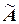 , построенная в ходе доказательства, называется присоединенной матрицей.
, построенная в ходе доказательства, называется присоединенной матрицей.
Следствие 2.9.1. У любой невырожденной матрицы 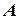 кроме
кроме 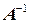 не существует других левых (правых) обратных матриц.
не существует других левых (правых) обратных матриц.
Доказательство. Пусть
 .
.
Поскольку по условию
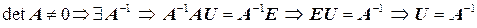 ,
,
 .
.
Следовательно, 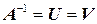 — единственная обратная матрица.
— единственная обратная матрица.
Следствие 2.9.2. Обратная матрица правой (левой) унитреугольной матрицы является правой (левой) унитреугольной матрицей.
Доказательство. Заметим, что определитель унитреугольной матрицы равен единице, поэтому соответствующая обратная матрица совпадает с присоединенной матрицей 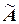 .
.
Рассмотрим произведение левой унитреугольной матрицы на матрицу 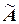 . Так как
. Так как 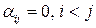 , то в соответствии с формулами (2.9.1) и (2.9.2) первая строка произведения
, то в соответствии с формулами (2.9.1) и (2.9.2) первая строка произведения  определяется соотношениями
определяется соотношениями
 ,
,
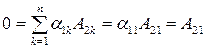 ,…,
,…,
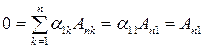 ,
,
т. е. имеем  = 1,
= 1, 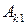 = 0, для любого
= 0, для любого 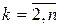 . Для второй строки имеем
. Для второй строки имеем
 ,
,
 ,
,
 , …,
, …,
 ,
,
таким образом, 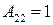 ,
, 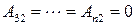 и т. д.
и т. д.
Теорема 2.9.2. Для любой невырожденной матрицы 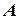 справедливы соотношения:
справедливы соотношения:
1. 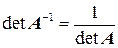 ;
;
2. 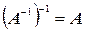 ;
;
3.  .
.
Доказательство.
1. 
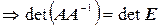
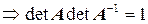 .
.
2. 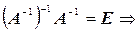


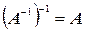 .
.
3. 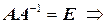
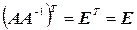


 .
.
Теорема 2.9.3. Для любых невырожденных матриц 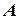 и
и  справедливо равенство
справедливо равенство
 .
.
Доказательство. По условию

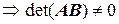
 .
.
Возьмем матрицу  и вычислим произведение
и вычислим произведение
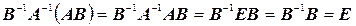 .
.
Следовательно,  — левая обратная матрица.
— левая обратная матрица.
Аналогично,
 .
.
Таким образом, матрица  одновременно является как правой, так и левой обратной матрицей, поэтому
одновременно является как правой, так и левой обратной матрицей, поэтому 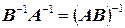 .
.
Теорема 2.9.4. Решение системы линейных уравнений  с квадратной невырожденной матрицей имеет вид
с квадратной невырожденной матрицей имеет вид 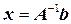 .
.
Доказательство. Пусть 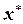 — решение системы. Тогда
— решение системы. Тогда


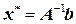 .
.
С другой стороны, если подставить 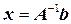 в систему, получаем равенство
в систему, получаем равенство  , т. е.
, т. е. 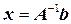 является решением системы.
является решением системы.
Найдем формулу построения обратной матрицы для ступенчатой матицы
 ,
,
где 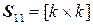 ,
,  , причем
, причем 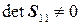 ,
,  . Тогда
. Тогда 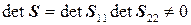 , поэтому у матрицы
, поэтому у матрицы  существует обратная матрица.
существует обратная матрица.
Допустим, что
 ,
,
причем 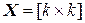 ,
,  . Тогда в соответствии с правилами умножения блочных матриц, имеем
. Тогда в соответствии с правилами умножения блочных матриц, имеем

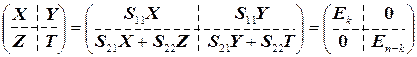 .
.
Сравнивая соответствующие блоки матриц, имеем следующие матричные соотношения
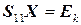 ,
,  = 0,
= 0, 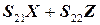 = 0,
= 0,  .
.
Рассмотрим последовательно данные равенства. Поскольку 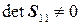 , то из первого соотношения следует, что
, то из первого соотношения следует, что  , а из второго —
, а из второго —  0. Тогда из последнего равенства с учетом невырожденности матрицы
0. Тогда из последнего равенства с учетом невырожденности матрицы 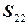 получаем
получаем 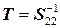 . Рассмотрим третье соотношение. Поскольку
. Рассмотрим третье соотношение. Поскольку  , то
, то  0. Выражая из полученного равенства матрицу
0. Выражая из полученного равенства матрицу  , имеем
, имеем  . Таким образом, окончательно получаем, что обратная матрица
. Таким образом, окончательно получаем, что обратная матрица
 .
.
|
|
|
|
|
Дата добавления: 2014-01-05; Просмотров: 2366; Нарушение авторских прав?; Мы поможем в написании вашей работы!