Евклидовы, нормированные и метрические пространства

Определение 3.17.1. Линейное n- мерное пространство называется евклидовым векторным n-мерным пространством, если в нем задана функция, сопоставляющая двум любым элементам a и b этого пространства вещественное число, называемое скалярным произведением и обозначаемое a × b, причем выполняются аксиомы:

12^°. a × b = b × a;

13^°. l (a × b) = (l a)×b;

14^°. (a + b)×c = a×c + b ×c;

15^°. a×a > 0, если a ¹ 0, a×a = 0, если a = 0.

Рассмотренные ранее линейные векторные пространства V ¹ ,V ² ,V ³ со скалярным произведением, определяемым по формуле 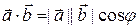, являются евклидовыми векторными пространствами соответственно размерностей 1, 2, 3.

Векторное пространство R n будет евклидовым n -мерным пространством, если ввести в нем скалярное произведение для его любых двух элементов a(a ₁, a ₂,…, a_n) и b(b ₁, b ₂,…, b_n) по формуле a×b =.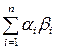

Определение 3.17.2. Два ненулевых элемента a и b евклидова пространства называются ортогональными, если равно нулю их скалярное произведение.

Заметим, что для геометрических векторов 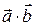= 0 тогда и только тогда, когда 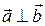, поэтому понятие ортогональности в пространствах 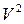и эквивалентно понятию перпендикулярности.

Теорема 3.17.1. Для любых двух элементов aи b произвольного евклидова пространства верно неравенство

(a×b)² £ (a×a)(b×b), (3.17.1)

называемое неравенством Коши-Буняковского.

Доказательство. На основании аксиомы 15° имеем

(l a – b)×(l a – b) ³ 0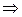 l ²(a×a) – 2 l (a×b) + (b×b) ³ 0.

Необходимым и достаточным условием неотрицательности квадратного трехчлена относительно l поскольку a×a > 0 является неположительность его дискриминанта, поэтому

(a×b)² – (a×a)(b×b) £ 0.

Теорема доказана.

Из неравенства Коши-Буняковского следует неравенство

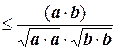–1 £ 1.

Следовательно, в любом евклидовом векторном пространстве можно определить

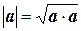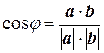
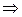
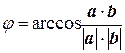, . (3.17.2)

В евклидовом точечном пространстве (в аффинном пространстве, в котором присоединенный линеал является евклидовым векторным пространством) можно находить расстояние между точками:

.

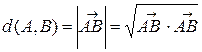Определение 3.17.3. Линейное n -мерное пространство L называется нормированным, если имеется правило, посредством которого всякому элементу x Î L ставится в соответствие вещественное число, называемое нормой указанного элемента и обозначаемое символом 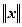, причем должны выполняться соотношения:

1. 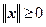, если x ¹ 0, 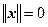, если x = 0;

2. 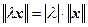для любого xÎ L и произвольного вещественного
числа l;

3. 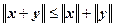для любых x, y Î L.

Теорема 3.17.2. Всякое евклидово пространство будет нормированным, если норму в нем определить равенством

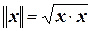. (3.17.3)

Доказательство. Справедливость для нормы (3.17.3) первых двух условий вытекает из соответствующих аксиом для скалярного произведения. Опираясь на неравенство Коши-Буняковского, убедимся в справедливости последнего неравенства. Действительно, из (3.17.1) следует, что 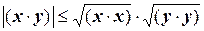. Тогда

.

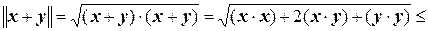
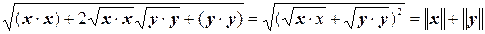Определение 3.17.4. Множество называется метрическим пространством, если каждой паре его элементов сопоставляется по некоторому правилу неотрицательное вещественное число, называемое расстоянием, причем справедливы соотношения:

1. r(x, y) > 0, если x ¹ y; r(x, y) = 0, если x = y;

2. r(x, y) = r(y, x);

3. r(x, y) £ r(x, z) + r(z, y).

Отметим, что нормированное пространство можно превратить в метрическое, если положить r(x, y) =.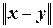

Линейное метрическое пространство легко превратить в нормированное, если положить 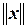=r(x, 0).

Дата добавления: 2014-01-05