Математичне дослідження дії не синусоїдної функції

План

Лекція №9

Питання самоконтролю

§ Яке призначення фільтру?

§ З яких елементів збирають електричну схему фільтрів, пояснити чому?

§ Які електричні схеми застосовуються при складанні фільтрів?

§ Що таке повздовжний опір у фільтрі?

§ Що таке опір поперек у фільтрі?

§ Що таке постійне число k у фільтрі?

§ Що таке область прозорості у фільтрі?

§ Що таке область згасання у фільтрі?

§ Що таке k фільтр?

§ Що таке m фільтр?

§ Перелічити та пояснити два основних положення для фільтрів?

§ Дати класифікацію фільтрів в залежності від діапазону частот?

§ Дати класифікацію параметрів фільтрів?

§ Що таке НЧ фільтри. Привести схему?

§ Що таке ВЧ фільтри. Привести схему?

§ Які важливі положення необхідні вважати при розрахунку фільтрів?

§ Що таке полосно пропускаючі фільтри?

§ Що таке полосно загороджуючі фільтри?

§ Що таке RC-фільтри?

§ При яких умовах застосовують RC-фільтри?

Тема: Кола змінного не синусоїдного струму.

1.Умови необхідності вивчення кіл не синусоїдного струму.

2. Математичне дослідження дії не синусоїдної функції.

3. Розрахунок кіл з не синусоїдними періодичними ЕРС та струмами

4. Приклад розв’язання задачі

5. Питання самоконтролю

1. Умови необхідності вивчення кіл не синусоїдного струму:

- недосконалість джерел напруги синусоїдальної форми, через те, що виникають різні спотворення;

- використання джерел, які видають явно не синусоїдальну форму напруги (струму), наприклад у вигляді прямокутника, трикутника, пилки, тощо;

- наявність у колі хоча б одного нелінійного елемента, або елемента з періодично змінним параметром.

Кола у разі наявності періодичної не синусоїдальної дії 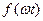досліджують на підставі його розкладу у ряд Ейлера-Фурьє:

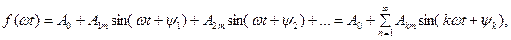
де 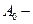стала складова, або нульова гармоніка; 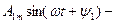основна, або перша гармоніка; 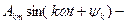вищі гармоніки при .

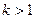Функція 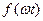при цьому повинна задовольняти умові Дирихле, т.б. мати на скінченому інтервалі скінчену кількість розривів першого роду і скінчену кількість максимумів та мінімумів. Функції, з якими мають справу електрики, цю умову задовольняють.

Якщо розписати синус суми, то ряд Ейлера-Фурьє можливо записати у другій модифікації:

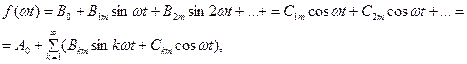
де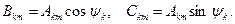

Слід зазначити, що періодичні функції простої геометричної форми (трапеція, пилка, тощо), з якими у ТОЕ пов’язані основні практичні задачі, вже давно розкладено в ряд Ейлера-Фурьє, і тому результати беруть з довідників.

Практикою розкладання встановлено, що функції, симетричні відносно вісі абсціс (рис.9.1), т.б. які задовольняють умові 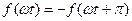, не містять сталої складової та парних гармонік;

Рис.9.1

Функції, симетричні відносно вісі ординат (рис.9.2), тобто які задовольняють умові 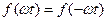, не містять синусних складових;

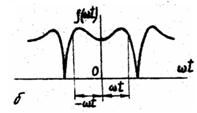
Рис.9.2.

Функції, симетричні відносно початку координат (рис.9.3), тобто які задовольняють умові 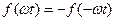, не містять сталої та косинусних складових;

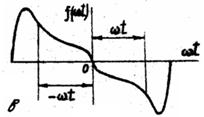
Рис.9.3.

Якщо початок відліку часу у функції зсувається, то її тригонометричний ряд зберігає значення амплітуд гармонік, але змінюються їх початкові фази. Наприклад, якщо перейти від функції 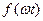, до 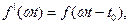отримаємо ряд:

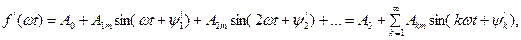
де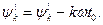

Сукупність гармонічних складових не синусоїдальної періодичної функції названо її дискретним частотним спектром. Він характеризується залежностями 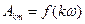та 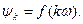Першу називають спектром амплітуд, друга – спектр фаз.

На малюнку рис.9.4. подано ілюстрацію спектра амплітуд для не синусоїдної функції у вигляді низки прямокутних імпульсів.

Рис.9.4.

Крім дискретного частотного спектра не синусоїдна періодична функція 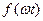описується значеннями та коефіцієнтами у таблиці 1.

Таблиця 1.

Значення та коефіцієнти	Позначення й математична форма запису	Позначення для синусоїдної функції
Максимальне значення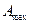
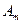
Діюче значення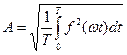
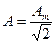
Діюче значення І-ї гармоніки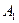
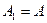
Діюче значення вищих гармонік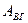
Середнє значення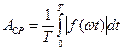
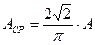
Середнє значення за половину періоду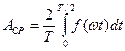
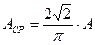
Коефіцієнт форми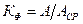
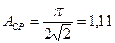
Коефіцієнт амплітуди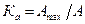
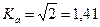
Коефіцієнт спотворень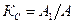
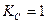
Коефіцієнт гармонік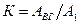

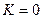
Діюче значення досліджуваної величини буде виглядати:

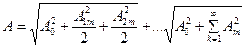
де значення вищих гармонік визначено за формулюванням:

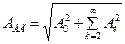
Дата добавления: 2014-01-05