
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Теорема Хеза
|
|
|
|
Декомпозиция без потерь и функциональные зависимости.
Теорема Хеза.
Название лекции: Декомпозиция без потерь и функциональные зависимости.
Лекция №14
План:
1. Декомпозиция без потерь и функциональные зависимости.
2. Теорема Хеза.
3. Предварительные (перед нормализацией) замечания о ФЗ. ФЗ как семантическое понятие.
Основной механизм нормализации – декомпозиция исходного отношения (проектирование исходного отношения).
Ясно, что получение новых отношений не должно приводить к потере информации (возникновению противоречий), т. е. соединение полученных проекций должно дать исходное отношение:
Пример:
| S: | Код | Статус | Город |
| Казань | |||
| Новгород |
| 1) | S11 | Код | Статус | S12 | Код | Город |
| Казань | ||||||
| Новгород |
| 2) | S21 | Код | Статус | S22 | Статус | Город |
| Казань | ||||||
| Новгород |
S11 JOIN S12: = S1
| Код | Статус | Город |
| Казань | ||
| Новгород |
S21 JOIN S22 ¹ S1 и содержит противоречивую информацию (нарушается условие один город – один поставщик).
Пусть R1 и R2 – проекции некоторого отношения R. Поставим задачу: Какие условия должны выполняться, чтобы при соединении отношений R1 и R2 получить исходное отношение R.
Решение поставленной задачи дает теорема Хеза (Heath).
Пусть R отношение с атрибутами {A, B, C}. Если R удовлетворяет зависимости A®R, т.е. (А ® В и А ® С), R = ABÈAC эквивалентно, т. к. А ® А по 4 правилу Амстронга,то R равно соединению его проекций {A, B} и {A, C}.
Рассмотрим предыдущий пример.
В исходном отношении, очевидно, есть две ФЗ: S={{код ® статус}{код ® город}}
Очевидно, что S – неприводимое множество ФЗ и по т. Хеза проекции {код, статус} и {код, город} дают исходное отношение {код, статус, город}.
Если рассмотреть проекции: {код, статус} и {статус, город}, то при таком разбиении утрачивается функциональная зависимость {код, город} и соединение проекций не дадут исходное отношение (транзитивности нет, т. к. статус ® город - нет).
Далее рассмотрение нормальных форм будем производить на примере следующего отношения:
поставщики + товары
| Код | Город | Товары | Количество |
| Москва | |||
| Москва | |||
| Москва | |||
| Москва | |||
| Москва | |||
| Москва | |||
| Ростов | |||
| Ростов | |||
| Ростов | |||
| Москва | |||
| Москва | |||
| Москва |
1. Предварительные (перед нормализацией) замечания о ФЗ. ФЗ как семантическое понятие.
1) Зависимости, отвечающие п.2. в определении неприводимых зависимостей, называются неприводимые слева, т.е. это те зависимости, у которых нельзя слева опустить ни одного атрибута, чтобы не изменилось замыкание множества функциональных зависимостей (левая часть каждой ФЗ должна быть предельно простой). Неприводимые ФЗ и неприводимые слева ФЗ играют важную роль в нормализации.
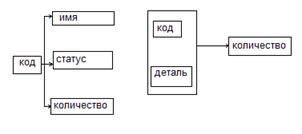
2) Для изображения ФЗ используется графическое изображение ФЗ, так называемая диаграмма ФЗ (или схема ФЗ).
Пример:
|
|
|
|
Дата добавления: 2014-01-05; Просмотров: 1158; Нарушение авторских прав?; Мы поможем в написании вашей работы!