Лекция №17. Название лекции: Нормальная форма Бойса – Кодда (НФБК)

Название лекции: Нормальная форма Бойса – Кодда (НФБК).

План:

1. Определение НФБК.

2. Примеры НФБК.

3. Преимущества НФБК.

1. Определение НФБК.

Рассмотрим более общий случай отношения.

Пусть:

1) Отношение имеет два (или более) потенциальных ключа.

2) Два потенциальных ключа является сложными.

3) Потенциальные ключи перекрываются

Замечание: отношения, у которых имеются условия 1, 2, 3, встречаются редко, если у отношения нет условий 1, 2, 3, то 3НФ совпадает с НФБК.

Отношение находится в нормальной форме Бойса-Кодда тогда и только тогда, когда каждая нетривиальная и неприводимая слева ФЗ обладает потенциальным ключом в качестве детерминанта.

Менее формальное определение имеет формулировку:

Отношение находится в НФБК тогда и только тогда, когда детерминанты являются потенциальными ключами.

На диаграммах ФЗ стрелки будут начинаться только с потенциальных ключей. Никакие другие стрелки не допускаются.

2. Примеры НФБК.

Рассмотрим отношение R₁

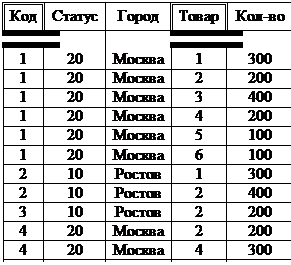Схема ФЗ имеет вид:

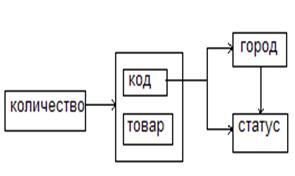
Детерминанты:{код}, {город}, {код, товар}, только {код, товар}→ потенциальный ключ. Таким образом отношение R₁ не находится в НФБК.

Отношение R₃, R₅ и R₆, которые находятся в 3НФ.

R₃:

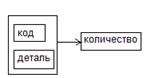
R₅: 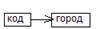R₆:

Эти отношения также находятся в НФБК, т.к. единственный потенциальный ключ является и единственным детерминантом.

Рассмотрим отношение: {код, имя-поставщика, статус, город}.

Допустим, что код и имя-поставщика являются потенциальным ключом (т.е. поставщик имеет уникальный код и уникальное имя).

Кроме того, пусть ФЗ город→статус не выполняется (ранее введенная такая зависимость использовалась только для иллюстрации).

Диаграмма ФЗ имеет вид:

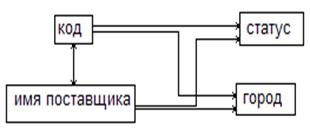
Все детерминанты являются потенциальными ключами. Отношение находится в НФБК.

Рассмотрим отношение: {код, имя-поставщика, товар, кол-во} предположим, что имена поставщиков и код являются уникальными.

Потенциальные ключи в этом отношении {код, товар} и {имя-поставщика, товар}, ясно, что имеется ФЗ код→имя_поставщика и имя_поставщика→код. Таким образом данное отношение не находится в НФБК, т.к. есть детерминанты которые не являются потенциальными ключами.

Пусть часть этого отношения имеет вид:

Это отношения обладает избыточностью => есть аномалии обновления, но заметим, что отношения находятся в ЗНФ т.к. для ЗНФ (в определении Кодда) требуется, чтобы каждый не ключевой атрибут неприводимо зависел от потенциального ключа, т.е. то, что атрибут имя_поставщика приводимо зависит от потенциального ключа {код, товар} игнорируется.

Для решения проблемы разобьем отношение на 2 проекции:

А: {код, имя_поставщика}, {код, товар, количество};

В: {код, имя_поставщика}, {имя_поставщика, товар, количество}.

Обе композиции находятся в НФБК.

Рассмотрим отношение: {студент, курс, преподаватель}.

(кортеж означает, что студент обучается предмету некоторым преподавателям).

Пусть накладываются некоторые ограничения:

1) Каждый студент, изучая данный предмет, обучается только одним преподавателем.

2) Каждый преподаватель ведет только один предмет (но каждый предмет может преподаваться несколькими преподавателями).

Схема ФЗ имеет вид:

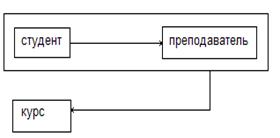
В рассматриваемом примере есть два перекрывающихся потенциальных ключа: {студент, курс} и {студент, преподаватель}. Отношение находится в ЗНФ, т.к. нет неключевых полей вообще, но не в НФБК опять есть аномалии удаления: удалив запись о том, что Петров изучает физику, удаляем сведения о том, что Лимонов преподает физику. Проблема в том, что {преподаватель} является детерминантом, но не является потенциальным ключом. Построим разбиение.

А: {студент, преподаватель} и {преподаватель, курс}

СТУДЕНТ	ПРЕПОДАВАТЕЛЬ		ПРЕПОДАВАТЕЛЬ	КУРС
Иванов	Белов	Белов	Математика
Иванов	Сидоров	Сидоров	Физика
Петров	Белов	Лимонов	Физика
Петров	Лимонов

Потенциальные ключи:

{студент, преподаватель} {преподаватель}

Отношения находятся в НФБК. Имеется естественная ФЗ {преподаватель}→{курс}. Кроме того, должно иметь место ФЗ связывающая отношения {студент, курс}→{преподаватель}.

Устранены некоторые противоречия (убрать запись Петров, Лимонов, но сведения о том, что Лимонов преподает физику останется). Но имеется другие проблемы: добавим запись Иванов, Лимонов.

Формально это можно сделать, но это противоречит тому, что Иванов уже изучает физику у Сидорова, т.е. эти два отношения связаны (не являются независимыми): ФЗ {студент, курс}→{преподаватель} нельзя получить из ФЗ этого разбиения (только одна ФЗ {преподаватель}→{предмет}, т.е. добавить запись в отношение 1 нельзя без проверки отношения 2). Таким образом декомпозиция на компоненты в НФБК и композиция на независимые компоненты может вступить в конфликт.

Рассмотрим отношения R с атрибутами: {студент, предмет, номер_в_списке}

Кортеж: (S,P,N)ÎR, если студент S сдает экзамен по предмету P, если он занесен в список сдающих под номером N.

Имеют места следующее ограничение: никакие два студента не могут иметь один и тот же номер по списку по одному и тому же предмету; имеют место следующие ФЗ: {студент, предмет}→{номер}, {предмет, номер}→{студент}

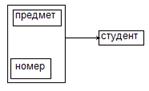
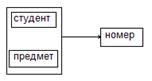
В отношении имеются два перекрывающихся ключа:{студент, предмет} и {предмет номер}, т.к. оба потенциальных ключа являются детерминантами и других детерминантов нет, то отношение находится в НФБК.

У этого отношения нет аномалий.

3. Преимущества НФБК.

1) Позволяет избавится от некоторых проблем, присущих (хотя бы теоретически) форме ЗНФ.

2) Определение НФБК концептуально проще ЗНФ (нет: 1НФ, 2НФ, первичного ключа, транзитивной зависимости).

Дата добавления: 2014-01-05