Шифрование методом перестановки. Маршруты Гамильтона. Аналитические методы шифрования

Шифрование методом полиалфавитной замены. Алгоритм полиалфавитной замены с использованием таблицы Вижинера.

В шифрах многоалфавитной замены, в отличии от описанных выше, для шифрования применяются несколько перемешанных алфавитов, поочередно используемых при замене букв исходного шифруемого сообщения.

К многоалфавитным шифрам относятся шифр Вижинера, шифр «Энигма», цилиндр Джефферсона и др. Использование шифра Вижинера, например, сво­дится к следующему. Множество, например, из 33 алфавитов (циклических сдвигов) русского языка формируется путем последовательного сдвига букв исходного алфавита, подобно рассмотренному выше шифру Цезаря.

Совокупность всех алфавитов, сведенных в одну таблицу, образует так называемую шифровальную таблицу Вижинера (рис. 5.16). При шифрова­нии в этом случае также имеется кодовое слово, буквы которого определя­ют выбор конкретного алфавита, используемого при замене соответству­ющей буквы открытого текста. Процесс шифрования может быть описан, в данном случае, как суммирование номеров соответствующих друг другу букв открытого текста и ключевого слова по модулю 33.

Рассмотрим пример формирования шифра Вижинера для использованных выше информационного сообщения и ключевого слова, повторяющегося не­обходимое число раз.

Исходное сообщение разбивается на блоки с использованием ключевого слова «КОРЕНЬ», которое записывается над исходным открытым текстом 5 раз подряд (для нашего текста). Выбираем строку с алфавитом, который начинается с буквы К (первая буква ключевого слова) в первом столбце шифровальной таблицы Вижинера (см. рис 5.16). Первая буква шифрован­ного текста находится на пересечении этой строки и столбца таблицы, на­чинающегося с первой буквы открытого текста (первая строка таблицы), в данном случае это буква Т. Следующая буква шифротекста находится на пересечении строки таблицы, начинающейся со второй буквы ключевого слова — буквы О, и столбца, начинающегося со второй буквы открытого текста. Это буква — О. Аналогично производится шифрование остальных букв. В итоге, получается шифротекст, по количеству символов совпадаю­щий с исходным открытым текстом:

ТОВЙСЬ ШУХЦЬН ЭЭЩЧЯЫ ТОТЧЮЬ ИАГЕЯЦ

На практике для повышения криптостойкости шифрования обычно исполь­зуют два общих принципа шифрования: рассеивание и перемешивание. Прин­цип рассеивания состоит в распространении влияния одного символа откры­того текста на некоторое, иногда большое, количество символов шифротек­ста, что позволяет скрыть статистические свойства открытого текста. Развитием этого принципа является распространение влияния одного символа ключа на много символов шифрограммы, что позволяет исключить вос­становление ключа по частям. Принцип перемешивания состоит в использовании таких шифрующих преобразований, которые исключают восстановле­ние взаимосвязи статистических свойств открытого и шифрованного текста.

Распространенный способ шифрования, при котором достигается хоро­шее рассеивание и перемешивание, состоит в использовании составного шифра. Этот шифр строится на основе совместного использования простых шифров замены и перестановки, каждый из которых вносит некото­рый вклад в значительное суммарное рассеивание и перемешивание.

Одним из наглядных примеров криптоалгоритма, разработанного в соответ­ствии с принципами рассеивания и перемешивания, может служить принятый в 1977 году Национальным бюро стандартов США стандарт шифрования данных DES. Несмотря на интенсивные и тщательные исследования алгоритма специалистами, пока не найдено уязвимых мест алгоритма, на основании которых можно было бы предложить метод криптоанализа, существенно лучший полного перебора ключей. В нашей стране введен в действие подобный отечественный криптоалгоритм шифрования – ГОСТ 28147-89.

В то же время, несмотря па широкое распространение блочного шифро­вания, ему присущи следующие недостатки:

• Одиночная ошибка в шифротексте вызывает искажение примерно половины открытого текста при дешифровании, что требует применения мощных кодов, исправляющих ошибки

• Из двух одинаковых блоков открытого текста получаются одинаковые блоки шифрованного текста.

Избежать этих недостатков позволяют поточные (потоковые) шифры

Шифры поточного (потокового) шифрования

В современных системах шифрования данных широкое применение нашли системы поточного (потокового) шифрования. Поточные (потоковые) шифры, в отличие от блочных, осуществляют поэлементное шифрование потоки данных без задержки в криптосистеме. В общем случае каждый символ от­крытого текста шифруется, передается и дешифруется независимо от других символов. Иными словами, шифрующее преобразование элемента открытого текста меняется от одного элемента к другому, в то время как для блочных шифров шифрующее преобразование каждого блока остается неизменным. В некоторых случаях символ открытого текста может шифроваться с учетом ограниченного числа предшествующих ему символов.

Важным достоинством поточного шифрования является высокая скорость преобразования данных, соизмеримая со скоростью поступления открытого текста, что обеспечивает шифрование и расшифрование передаваемой информации больших объемов практически в реальном масштабе времени. Системы поточного шифрования обладают высокой криптостойкостью, так как вскрытие такой системы предполагает точное определение структуры генератора ключевой последовательности (ГКП) и его начальной фазы. Перечисленные положительные качества поточного шифрования в совокуп­ности с простой и низкой стоимостью технической реализацией поставили его в ряд наиболее перспективных систем шифрования.

Поточные (потоковые) шифры основываются на использовании ключе­вой последовательности с заданными свойствами случайности и двоичном (цифровом) представлении информационных сообщений. Шифрование н расшифрование осуществляется, как правило, с использованием операции сложения по модулю 2 элементов открытого текста и псевдослучайной ключевой последовательности. Последние состоят из сгенерированных определенным образом последовательностей символов с заданными свойствами непредсказуемости (случайности) появления очередного символа.

Рис.5.18. Шифр Вернама

Исторически первым поточным шифром стал шифр Вернама, в котором и качестве ключевой последовательности использовалась уникальная слу­чайная гамма. При этом размер ключа соответствовал длине ключевой последовательности. Принцип шифрования и расшифрования данных изобра­жен на рис. 5.18.

Отличительной особенностью шифра Вернама является шифрование гам­мы ключевых последовательностей, каждая из которых представляет собой шифр. Практическая реализация этого шифра из-за сложности реализации сверхдлинных ключевых последовательностей и неудобства их хранения оказалась затруднительной.

Более удобными оказались поточные шифры, в которых в качестве ключевых используются псевдослучайные последовательности (ПСП), формируе­мые генераторами ПСП. В этом случае секретный ключ определяется началь­ным состоянием генератора ПСП, а его размер значительно меньше размера открытого текста, что существенным образом упрощает решение задач техни­ческой реализации, хранения и передачи ключа.

В настоящее время существует достаточно большое количество поточных шифров, отличающихся друг от друга некоторыми отличительными признака­ми. Например, по способу синхронизации поточные шифры подразделяют­ся на синхронные и самосинхронизирующиеся.

Синхронные поточные шифры

В синхронных поточных шифрах ключевая последовательность или, как ее еще называют, гамма, формируется независимо от последователь­ности символов открытого текста и каждый символ этого текста шифру­ется независимо от других символов, а ключом Z является начальная ус­тановка генератора ПСП. Процесс шифрования и расшифрования при этом описывается выражениями:

yi=хi Е Fi(Z) — шифрование;

хi=уi Е Fi(Z) — расшифрование,

где уi,хi — двоичные символы зашифрованного и открытого текста, Fi(Z) — i-й символ ПСП, вырабатываемый генератором с функцией об­ратной связи F и начальным состоянием Z.

Синхронные поточные шифры можно классифицировать по способам построения ПСП, по соотношению размеров открытого текста и периода ключевой ПСП, по способам технической реализации.

По способам построения ПСП для синхронного шифрования различают:

• Метод комбинирования ПСП

• Метод функциональных отображений.

Суть первого метода заключается в построении комбинированных схем, представляющих собой совокупность регистров сдвига с линейными обрат­ными связями. Примерами таких схем являются схема Джеффра (рис. 5.20 а) и схема Брюс (рис. 5.20 б).

Отличие этих двух схем состоит в использовании для формирования ПСП различных логических устройств. Так, в схеме Джеффа применяется операция логического умножения и сложения по модулю 2. Схема Брюс использует пороговое устройство, работающее по правилу: на выходе 1, если порог превышен, иначе — 0.

Более сложным является метод функциональных отображений, суть ко­торого заключается в следующем. Пусть дано некоторое векторное про­странство GF(2m) с числом координат m в каждом векторе, причем каждая координата вектора принадлежит множеству скалярных величин GF(2)={0,1}. Очевидно, что общее число векторов, принадлежащих про­странству GF(2m), равно 2т. Пусть задано некоторое функциональное ото­бражение f, которое каждому вектору из векторного пространства GF(2m) ставит в соответствие вектор из пространства GF(2k). При этом обязатель­ным является выполнение условия k<=m. Далее пусть задано некоторое функциональное отображение g, которое каждому вектору из GF(2k) ставит в соответствие скаляр из множества GF(2). В этом случае получим ПСП с использованием вышеприведенных функциональных отображений. Например, ПСП, полученная по схеме, изображенной на рис. 5.21 (m=4, k 2), построена по методу двухступенчатых отображений.

Рис. 5.19. Классификация синхронных поточных шифров

Рис. 5.20. Схема Джеффа (а) и схема Брюс (б)

Метод ступенчатого отображения GF(2m) — GF(2k) — GF(2) впервые Пил использован при построении последовательностей Гордона-Милса-Велга. Для порождения векторного пространства GF(2m) использовались регистры сдвига с линейными обратными связями длины m с обратной свя­зью.

Следует заметить, что на практике имеет место различное число функцио­нальных отображений. С возрастанием используемых ступеней уровень криптостойкости шифрования повышается.

По отношению размера открытого текста и периода ключевой ПСП разли­чают схемы:

• С «бесконечной» ключевой ПСП (период ПСП больше размера открытого текста)

• С конечной ключевой ПСП или с режимом «бегущего кода» (пе­риод ПСП равен размеру открытого текста).

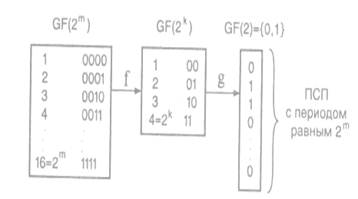
Рис. 5.21. Принцип формирования ПСП по методу двухступенчатых отображений

Рис. 5.22. Схема с нелинейной внешней (а) и внутренней (б) логикой

Схемы с «бесконечной» ключевой ПСП обладают более высокой криптостойкостью относительно вскрытия их структуры при известном откры­том тексте. Однако при вскрытии структуры ПСП по частично известному тексту схема «бегущий код» не позволяет вскрывать весь текст, а только его небольшую часть, поэтому разработчики спутниковой системы «Навстар» в качестве криптостойкой ПСП Р-кода использовали сегменты дли­тельностью 7 суток, выделенные случайным образом из нелинейной ПСП с периодом 267 суток.

По способам технической реализации синхронных поточных шифров можно выделить схемы, представленные на рис. 5.22:

• С нелинейной внешней логикой

• С нелинейной внутренней логикой.

При использовании нелинейной внешней логики основу генератора ПСП составляет регистр сдвига с линейными обратными связями, который по­рождает все ненулевые элементы векторного пространства GF(2n).

В схеме с нелинейной внутренней логикой генератор ПСП представля­ет собой регистр с нелинейными обратными связями. Такой генератор вы­рабатывает последовательности де Брейна с периодом 2n. Такие последо­вательности обладают одними из самых высоких показателей криптостойкости из всех классов ПСП, так как каждая серия из n-символов встречается на периоде ПСП только один раз.

Дата добавления: 2014-01-05