Распределение Больцмана

Как мы рассмотрели ранее, микропараметры системы многих частиц являются случайными величинами и для определения их значений нужно знать функции распределения.

Существует различные функции распределения. В классической физике используется классическая статистика Максвелла-Больцмана, в которой движение частиц определяется законами Ньютона, частицы считаются различимыми.

Это распределение частиц по энергиям.

Пусть система состоит из 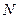материальных точек. Для каждой 3 скорости и 3 координаты. Разобьем все координатное пространство и пространство скоростей на 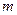участков и будем определять число частиц координаты и скорости которых попали в участок от до и от до . Энергия частиц подгруппы:

, где - энергия 1 частицы группы.

Энергия всей системы , где

Определим статистический вес состояния из 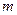групп по частиц (число размещений). Математика (комбинаторика) дает формулу:

, подставим это выражение в формулу Больцмана:

.

Учтем формулу Стирлинга для вычисления факториала:

при

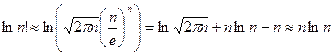
при величиной можно пренебречь.

Тогда

У нас идеальный газ находится в фиксированном объеме. Запишем изменение энергии, связанное с тем, что меняется число частиц в группе.

Основное ТД тождество для открытой системы :

, так как , то

В нашем случае, изменение внутренней энергии частиц в группе и изменение числа частиц в группе связаны: ; , отсюда изменение энтропии, связанное с тем, что меняется число частиц в группе:

Подставим полученное выражение в основное ТД тождество для открытой изохорической системы:

сгруппируем

отсюда

. Теперь выразим отношение :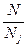

, Þ

, следовательно

, так как величина , то можно ее обозначить , тогда с учетом, того что вероятность частицы попасть в участок, мы получим распределение Больцмана: - вероятность того, что молекула идеального газа имеет энергию, т.е. находиться в -ом состоянии. Это дискретное распределение, но его можно сделать непрерывным.

В данном распределении остается скрытой предпосылка осуществления этого распределения – различимости частиц. Эта предпосылка с физической точки зрения ошибочна, потому что в природе нет различимых частиц, и все реально существующие частицы описываются либо распределением Ферми-Дирака, либо распределением Бозе-Эйнштейна. Однако в наиболее часто встречающихся ситуациях классической физики распределения Ферми-Дирака и Бозе-Эйнштейна практически совпадают с распределением Максвелла-Больцмана, которое благодаря этому является основным распределением классической статистической физики.

Дата добавления: 2014-01-05