Распределение энергии по степеням свободы

Среднее значение энергии одной молекулы . Если бы мы посчитали отдельно , то получили бы величину ровно в три раза меньшую, чем полная энергия. Такие же значения и для .

Таким образом, если вы молекула могла двигаться только вдоль оси , ее средняя энергия была бы . Говорят, что у молекулы, которая может совершать только одномерные движения – одна степень свободы: . Это значит. Что нужна только одна переменная, чтобы описать движение частицы. Для материальной точки таких переменных нужно 3: . Если же молекула может еще и вращаться, то число степеней свободы увеличивается. Средняя энергия, приходящаяся на одну степень свободы вращательного движения, а также на одну колебательную степень свободы (как потенциальной, так и кинетической) равна .

Теорема о равнораспределении энергии по степеням свободы: на все степени свободы статистической системы приходится одна и та же энергия . Это не относится к потенциальной энергии системы во внешних полях.

Средняя энергия одной молекулы , где число степеней свободы .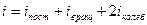

Расхождение теории теплоемкости идеального газа с экспериментом.

Например, для некоторого количества идеального газа: 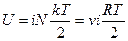, его молярная теплоемкость

Для двух атомных молекул всего может быть 3-поступательных, 2-вращательных, 1-колебательная степени свободы. По расчетам для водорода (идеального газа) теплоемкость не зависит от температуры .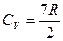

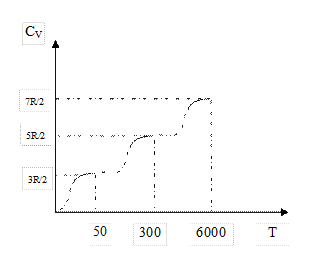
Зависимость теплоемкости молекулярного водорода от температуры, полученная в ходе экспериментов, дается на графике .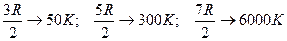

Молекула водорода ведет себя при низкой температуре как точечная частица, у которой отсутствуют внутренние движения, при нормальной температуре – как жесткая гантель и наряду с поступательным движением также совершает вращательные движения, а при очень высокой температуре к этим движениям добавляются также колебательные движения атомов, входящих в молекулу. Объяснить эту зависимость классической теории не удалось.

Отличие экспериментальной кривой от теоретической прямой имеет квантовое объяснение. При низких температурах вращательные и колебательные степени свободы «выключены», т.е. они не возбуждаются. При температурах ~116К могут возбуждаться вращательные степени свободы, а при температурах ~ 4100К возбуждаются и колебательные степени свободы. Однако переход от одного режима движения к другому происходит не скачком при определенной температуре, а постепенно в некотором интервале температур. Это объясняется тем, что при определенной температуре возникает лишь возможность перехода молекул в другой режим движения, но эта возможность не реализуется сразу всеми молекулами, а лишь их частью.

Дата добавления: 2014-01-05