Влияние способов закрепления стержня

Задача Эйлера определения критической силы

Для балки, изображенной на рисунке 9.2, проведем сечение на расстоянии z и рассмотрим равновесие изогнутой части

Рис. 9.2

Здесь R_z = P – равнодействующая внутренних сил. Сумма моментов относительно поперечной оси сечения

.

Поскольку изгибающий момент в сечении связан с прогибом дифференциальным уравнением

,

то получаем

.

Обозначим , тогда получим уравнение Эйлера

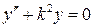. (9.1)

Общее решение (9.1) имеет вид:

. (9.2)

Константы a, b определяются из граничных условий

1.
.

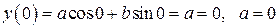2.
.

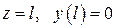
Последнее уравнение имеет два решения: и . Случай дает согласно найденному 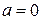и решению (9.2) нулевое значение . Этот случай соответствует условию отсутствия прогибов балки и, следовательно, процессу сжатия стержня без изгиба. Поскольку нас интересует определение критической силы при потере устойчивости, то рассмотрим второе решение: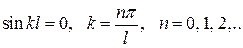

Далее получаем

.

Отсюда находим значение критической силы

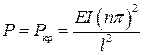. (9.3)

Критическая сила пропорциональна жесткости стержня на изгиб и обратно пропорциональна квадрату длины стержня.

Относительно выбора момента инерции в решении (9.3) заметим следующее. Если моменты инерции относительно двух главных центральных осей инерции поперечного сечения не равны между собой, то продольный изгиб произойдет в плоскости наименьшей жесткости, то есть поперечные сечения стержня будут поворачиваться вокруг той оси, относительно которой момент инерции имеет минимальное значение. Следовательно, вместо I нужно использовать I _min.

С практической точки зрения интерес представляет наименьшее значение критической силы, при которой происходит потеря устойчивости. При n = 1 в (9.3) получаем

.

Чаще всего концы стержня закрепляют одним из четырех способов, показанных на рисунке 9.3.

Рис. 9.3

Второй способ – шарнирное закрепление концов – рассмотрен в решении Эйлера.

При других способах закрепления используется обобщенная формула Эйлера

. (9.4)

где - коэффициент приведения длины стержня.

Значения коэффициента при других способах закрепления приведены в литературе.

Дата добавления: 2014-01-05