Формування бінарного дерева

При формуванні бінарного дерева треба задати деякі обмеження. Розглянемо приклад, коли необхідно побудувати дерево з n вершин, що має мінімальну висоту. Для досягнення мінімальної висоти необхідно, щоб всі рівні дерева, крім, можливо, останнього, були заповнені. Щоб зробити такий розподіл, всі вершини треба розподіляти порівно: ліворуч і праворуч.

Отже, правила для рівномірного розподілу при відомій кількості вузлів n можна сформулювати за допомогою подальшого рекурсивного алгоритму:

ü взяти один вузол як корінь;

ü побудувати ліве піддерево з кількістю вузлів n _l = [ n / 2] тим самим способом;

ü побудувати праве піддерево з кількістю вузлів n_r = n – n_l – 1 тим самим способом.

Опис вузла дерева мовою Turbo Pascal та додавання вузла виглядає так:

Type ElPtr = ^Element

Element = record

Data: integer;

L_Son, R_Son: ElPtr;

end;

Function Tree (n: integer): ElPtr;

var nl, nr, x: integer;

NewElement: ElPtr;

begin

if n=0 then Tree:=nil else begin

nl:=n div 2;

nr:=n – nl – 1;

read (x); New (NewElement);

with NewElement do begin

Data:=x;

L_Son:=Tree (nl);

R_Son:=Tree (nr);

end;

Tree:=NewElement;

end;

end;

Ефективність рекурсивного визначення полягає в тому, що воно дозволяє за допомогою кінцевого висловлення визначити нескінченну множину об’єктів.

6.1.5. Застосування бінарних дерев в алгоритмах пошуку

В однозв’язному списку неможливо використати бінарні методи, вони можуть використовуватися тільки в послідовній пам’яті. Однак, якщо використати бінарні дерева, то в такій зв’язній структурі можна одержати алгоритм пошуку зі складністю O (log ₂ N). Таке дерево реалізується в такий спосіб: для будь-якого вузла дерева із ключем T_i всі ключі в лівому піддереві повинні бути менші від T_i, а в правому – більше T_i. У дереві пошуку можна знайти місце кожного ключа, рухаючись, починаючи від кореня й переходячи на ліве або праве піддерево, залежно від значення його ключа. З n елементів можна організувати бінарне дерево (ідеально збалансоване) з висотою не більшою ніж log ₂ N, що визначає кількість операцій порівняння при пошуку.

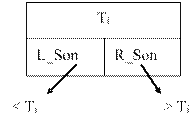
Function Search (x: integer; t: ElPtr): ElPtr;

{поле Data замінимо на поле Key}

var f: boolean;

begin

f:=false;

while (t<>nil) and not f do

if x=t^. Key then f:=true

else

if x>t^. Key then

t:=t^. R_Son

else

t:=t^. L_Son;

Search:=t;

end;

Якщо одержимо, що значення функції = nil, то ключа зі значенням x у дереві не знайдено.

Function Search (x: integer; t: ElPtr): ElPtr;

begin

S^.key:=x;

while t^.key<>x do

if x > t^.key then

t:=t^. R_Son else t:=t^. L_Son;

Search:=t;

end;

6.1.6. Операція включення в СД типу «бінарне дерево»

Побудова частотного словника

Розглянемо випадок дерева, що постійно зростає. Гарним прикладом цього є побудова частотного словника. У цій задачі задана послідовність слів і треба встановити кількість появи кожного слова. Це означає, що, починаючи з порожнього дерева, кожне слово, що зустрічається в тексті, шукається в ньому. Якщо це слово знайдене, то лічильник появи цього слова збільшується; якщо ж слово не знайдене, то в дерево включається нове слово зі значенням лічильника = 1.

Type ElPtr = ^Element

Element = record

Key: integer;

n: integer;

L_Son, R_Son: ElPtr;

end;

Procedure Put (x: integer; var t: ElPtr);

begin

if t=nil then

begin

New(t);

with t^ do begin

key:=x; n:=1;

L_Son:=nil;

R_Son:=nil;

end;

end

else

if x> t^.key then Put(x, t^.R_Son)

else

if x<t^.key then Put(x, t^.L_Son)

else t^.n:=t^.n+1;

end;

Хоча задача цього алгоритму – пошук із включенням, але його можна використати й для сортування, тому що він нагадує сортування із включенням. А тому, що замість масиву використається дерево, то пропадає необхідність переміщення елементів вище місця включення. Щоб сортування цього алгоритму було стійким, алгоритм повинен виконуватися однаково як при t ^. key=x, так і при t ^. key > x.

Нехай задана послідовність: 30, 1, 15, 17, 18, 50, 2, 60. Після побудови дерева здійснюється проходження дерева в симетричному порядку: 1, 2, 15, 17, 18, 30, 50, 60.

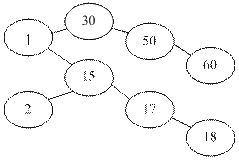
Аналіз алгоритму пошуку

Якщо дерево вироджується в послідовність, то складність у такому випадку O (N) (у найгіршому разі). У кращому ж випадку, якщо дерево збалансоване, то складність буде O(log ₂ N). Отже, маємо:

O(N) £ П_ФВС £ O(log ₂ N).

Якщо вважати, що ймовірність появи будь-якої структури дерева однакова, і ключі з’являються з однаковою ймовірністю, то .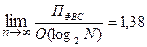

Алгоритм сортування є стійким, якщо елементи з однаковими ключами з’являються в тій же послідовності при симетричному обході дерева, що й у процесі їхнього включення в дерево.

6.1.7. Операція виключення з бінарного дерева

При видаленні вузла дерево має залишатися впорядкованим щодо ключа:

а) видаляється аркуш;

б) видаляється вузол з одним нащадком (нащадок ліворуч або праворуч);

в) видаляється вузол із двома нащадками, але в лівому нащадку немає правого піддерева;

г) загальний випадок.

Розглянемо випадок б):

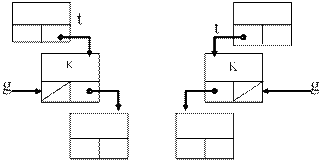
if g^.L_Son=nil then begin

g:=t;

t:=t^.R_Son;dispose(g);

end;if g^.R_Son=nil then begin

g:=t;

t:=t^.L_Son;

dispose(g);

end;

Випадок а) є частковим випадком цього алгоритму.

Випадок в): r вказує на елемент, що не має правого піддерева.

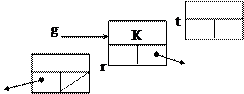g:=t;

g^.key:=r^.key;

g:=r;

r:=r^.L_Son;

dispose(g);

Ми шукаємо такий елемент, у якого відсутнє праве піддерево (на такий елемент вказує r). Послідовність операторів та сама, тобто видаляє элемент, який треба замінити найбільш правим елементом його лівого піддерева. Такі елементи не можуть мати більше одного нащадка.

t

Випадок г):

Procedure Get (x: integer; var t: ElPtr);

var g: ElPtr;

begin

if t=nil then

{опрацювання виняткової ситуації, коли елемента із заданим ключем у дереві немає}

else if x>t^.key then Get(x, t^.R_Son)

else if x<t^.key then Get(x, t^.L_Son)

else begin

g:=t;

if g^.L_Son=nil then t:=g^.R_Son

else if g^.R_Son=nil then t:=g^.R_Son

else D(g^.L_Son); {знайти r)

dispose(g);

end;

end;

Дата добавления: 2014-01-05