Додавання елемента

Процедура починається аналогічно до додавання елемента в бінарне дерево, пошуку та фарбування її у червоний колір. Подальші дії залежать від кольорів сусідніх вершин. Зазначимо, що:

ü властивість 2 завжди зберігається,

ü властивість 3 порушується тільки при додаванні червоної вершини, перефарбуванні чорної вершини в червону або обертанні,

ü властивість 4 порушується тільки при додаванні чорної вершини, перефарбуванні червоної вершини в чорну або обертанні.

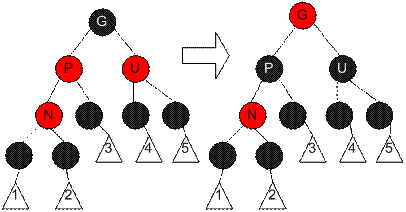
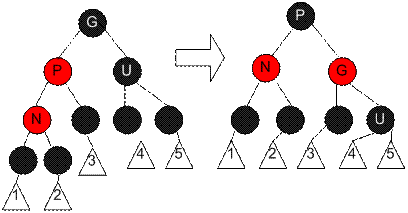
На допоміжних діаграмах, вершина, яка додається, позначена N, первісний батько цієї вершини позначений P, батько вершини P («дідусь» N) позначений G. «Дядько» N (тобто вершина, яка має спільного з P батька – G) позначений як U. Розглянемо подані випадки.

Випадок 1. Нова вершина розташована в корені дерева. У такому випадку необхідно пофарбувати її в чорний колір для забезпечення властивості 1. Очевидно, що властивість 5 при цьому залишається справедливою.

Випадок 2. Батько нової вершини є чорним. Властивість 3 не порушена. У цьому випадку дерево є коректним. Властивість 5 також зберігається, адже червона вершина додається на місце чорного листка і це не змінює кількості чорних вершин на цьому шляху.

Випадок 3. Батько та дядько доданої вершини є червоними. Тоді ми можемо перефарбувати їх обох в чорний колір, а також перефарбувати дідуся в червоний. Тепер наша червона вершина має чорного батька. Завдяки тому, що будь-який шлях через батька чи дядька повинен проходити і через дідуся, кількість чорних вершин на шляху залишається незмінною. Однак батько дідуся (тобто прадідусь) може бути червоною вершиною, як тепер і дідусь. Якщо це так, слід повторити цю операцію рекурсивно.

Зауваження: У наступних випадках ми припускаємо, що вершина P є лівим нащадком G. Якщо P – правий нащадок, ліву та праву вершини в аналізі поданих далі випадків треба поміняти місцями.

Випадок 4. Батько є червоним, але дядько – чорний. До того ж, нова вершина – правий нащадок свого батька, і батько, в свою чергу, лівий нащадок свого батька. У такому випадку, ми можемо виконати лівий поворот, внаслідок якого нова вершина та її батько поміняються ролями. Подальші дії з колишнім батьком виконуються відповідно до випадку 5. Зважаючи на те, що нова вершина та її батько є червоними, операція повороту не змінює умови 4.

Випадок 5. Батько є червоним, але дядько чорний. До того ж, нова вершина – лівий нащадок свого батька, і батько є лівим нащадком свого батька. У такому випадку ми виконуємо правий поворот навколо дідуся. Як результат колишній батько тепер є батьком і нової вершини, і свого бувшого дідуся. Ми знаємо, що бувший дідусь є чорним, інакше батько не був би червоним. Тепер треба поміняти місцями кольори бувшого батька та дідуся, і тепер для дерева виконується властивість 3. Як бачимо, властивість 4 також залишається незмінною.

Функція додавання вершини у червоно-чорне дерево:

Type link=^l;

l=record {структура для описування червоно-чорного дерева}

key:integer; {значення ключа}

red:boolean; {якщо вершина червона, true, інакше false}

l,r:link; {лівий та правий сини}

end;

Var head, w: link;

k: integer;

st1: string;

Function rotate(v:integer;y:link):link; {функція повороту}

Var c,gs:link;

begin

{обираємо напрямок руху}

if v<y^.key then c:=y^.l else c:=y^.r;

if v<c^.key then

begin

{здійснюємо обмін вершинами }

gs:=c^.l; c^.l:=gs^.r; gs^.r:=c;

end else

begin

gs:=c^.r; c^.r:=gs^.l; gs^.l:=c;

end;

if v<y^.key then y^.l:=gs else y^.r:=gs;

rotate:=gs;

end;

Function split(v: integer; m,p,g,gg: link):link;

{перефарбування вершини}

begin

m^.red:=true; m^.l^.red:=false; m^.r^.red:=false;

if p^.red then

begin

g^.red:=true;

if (v < g^.key) <> (v < p^.key) then

p:=rotate(v,g);

m:=rotate(v,gg); m^.red:=false;

end;

head^.r^.red:=false;

split:=m;

end;

Function insert(v: rec; n: link):link;

{lдодавання вершини}

Var q1,q2,p: link;

begin

p:=n; q1:=p;

repeat

q2:=q1; q1:=p;

p:=n;

if v<n^.key then n:=n^.l Else n:=n^.r;

if n^.l^.red And n^.r^.red then n:=split(v,n,p,q1,q2);

until n^.l=n;

New(n);

n^.key.fio:=v.fio;

n^.l:=n;

n^.r:=n;

if v<p^.key then p^.l:=n else p^.r:=n;

insert:=n;

n:=split(v,n,p,q1,q2);

End;

Дата добавления: 2014-01-05