
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Свойства сравнений
|
|
|
|
1. Для всякого целого с a º b (mod m) Û a ± c º b ± c (mod m), то есть к обеим частям сравнения можно прибавить или вычесть из обеих частей одно и то же целое число.
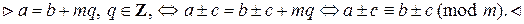
2. Сравнения можно почленно складывать и вычитать: a º b (mod m) & c º d (mod m) Þ a ± c º b ± d (mod m).
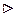
 &
& 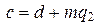 ,
,  Þ
Þ  ,
, 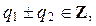 Û
Û  .
.
3. Сравнения можно почленно перемножать: a º b (mod m) & c º d (mod m) Þ a × c º b × d (mod m).
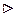
 &
& 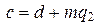 ,
, 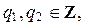 Þ
Þ 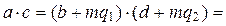
 ,
,  Û
Û  .
.
4. Следствие из свойства 3. Сравнения можно почленно возводить в любую натуральную степень: a º b (mod m) Þ an º bn (mod m) для 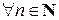 .
.
5. Если в сравнении числа a, b, m имеют общий делитель d, то на него обе части сравнения и модуль можно сократить: a º b (mod m) Û a / d º b / d (mod m / d).
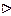
 .
.
6. Обе части сравнения можно сократить на их общий множитель, взаимно простой с модулем: если a = a 1 × d, b = b 1 × d, (d, m) = 1, то a º b (mod m) Û a 1 º b 1 (mod m).
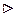
 ,
, 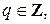 Þ
Þ 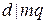 по свойству 6 делимости целых чисел, но так как (d, m) = 1, то
по свойству 6 делимости целых чисел, но так как (d, m) = 1, то  по свойству 2 взаимно простых чисел, значит q = q 1 × d, q 1 Î Z. Таким образом, a º b (mod m) Û
по свойству 2 взаимно простых чисел, значит q = q 1 × d, q 1 Î Z. Таким образом, a º b (mod m) Û  Û
Û 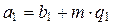 Û
Û  (mod m).
(mod m).
Легко проверяются следующие три свойства.
7. Рефлексивность: для любого целого а и всякого натурального m a º a (mod m).
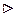 Действительно, a – a = 0 и m | 0 по свойству 1 делимости целых чисел.
Действительно, a – a = 0 и m | 0 по свойству 1 делимости целых чисел.
8. Симметричность: a º b (mod m) Û b º a (mod m).
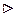 m | (a – b) Û m | (b – a) по свойству 7 делимости целых чисел.
m | (a – b) Û m | (b – a) по свойству 7 делимости целых чисел.
9. Транзитивность: если a º b (mod m) и b º c (mod m), то a º c (mod m).
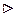 a – c = (a – b) + (b – c), m | (a – b) & m | (b – c) Þ m | (a – c) по свойствам 5 и 6 делимости целых чисел.
a – c = (a – b) + (b – c), m | (a – b) & m | (b – c) Þ m | (a – c) по свойствам 5 и 6 делимости целых чисел.
Свойства 7–9 означают, что отношение сравнимости на множестве целых чисел Z есть отношение эквивалентности. Это означает, что Z разбивается на непересекающиеся классы попарно сравнимых друг с другом по модулю 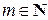 целых чисел.
целых чисел.
Каждый класс сравнимых друг с другом целых чисел характеризуется общими свойствами представителей этого класса. Например, все они имеют один и тот же остаток от деления на модуль; все они в силу теорем 1.6.1 и 1.2.1 имеют одинаковый наибольший общий делитель с этим модулем.
 ,
, 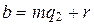 , где
, где 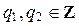 ,
,  .
.
 , где
, где  , Þ (a, m) = (m, b).
, Þ (a, m) = (m, b).
§1.7. Множество классов вычетов
При делении целых чисел на натуральное число m существует m различных остатков: 0, 1, 2,…, m – 1. Соответственно этим остаткам Z разбивается на m непересекающихся классов сравнимых друг с другом чисел, имеющих, как отмечено в §1.6, один и тот же остаток от деления на m. В соответствии с остатками от деления на m эти классы будем обозначать 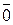 ,
, 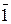 ,…,
,…, 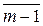 . Таким образом, класс
. Таким образом, класс 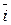 = {
= {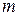 ×
×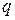 +
+  |
| 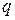 Î Z } для каждого
Î Z } для каждого  = 0, 1, 2,…, m – 1. Любой представитель класса однозначно определяет свой класс, то есть для каждого
= 0, 1, 2,…, m – 1. Любой представитель класса однозначно определяет свой класс, то есть для каждого 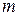 ×
×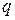 +
+  класс
класс  =
=  .
.
Поскольку остаток по-английски – «residue» – переводится на русский язык еще и как «вычет», то множество всех классов сравнимых друг с другом чисел по модулю m называют множеством классов вычетов по модулю m и обозначают Z / m Z. Таким образом, Z / m Z = 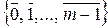 – множество из m элементов. Заметим, что для любых классов
– множество из m элементов. Заметим, что для любых классов 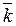 ,
,  Î Z / m Z и для произвольных k 1, k 2 Î
Î Z / m Z и для произвольных k 1, k 2 Î  , l 1, l 2 Î
, l 1, l 2 Î  суммы k 1 + l 1 и k 2 + l 2 принадлежат одному классу из Z / m Z, так как эти суммы сравнимы друг с другом по модулю m согласно свойству 2 сравнений из §1.6. Аналогично, согласно свойству 3 сравнений из §1.6 произведения k 1 × l 1 и k 2 × l 2 находятся в одном классе из Z / m Z.
суммы k 1 + l 1 и k 2 + l 2 принадлежат одному классу из Z / m Z, так как эти суммы сравнимы друг с другом по модулю m согласно свойству 2 сравнений из §1.6. Аналогично, согласно свойству 3 сравнений из §1.6 произведения k 1 × l 1 и k 2 × l 2 находятся в одном классе из Z / m Z.
 Определим операции сложения и умножения на Z / m Z. Полагая, что сумма
Определим операции сложения и умножения на Z / m Z. Полагая, что сумма  +
+  =
= 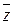 , где
, где  – такой единственный класс из Z / m Z, в который попадают все суммы
– такой единственный класс из Z / m Z, в который попадают все суммы  +
+ 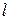 для k Î
для k Î  , l Î
, l Î  , а произведение
, а произведение  ×
× =
=  – тот единственный класс из Z / m Z, в который попадают все произведения k × l для k Î
– тот единственный класс из Z / m Z, в который попадают все произведения k × l для k Î  , l Î
, l Î  .
.
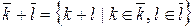 ,
,  .
.
Поскольку сложение и умножение в Z / m Z однозначно определяются сложением и умножением представителей классов вычетов, то свойства 1–5 операций сложения и умножения в Z из §1.1 справедливы и в Z / m Z.
1.  +
+ 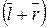 =
= 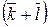 +
+ 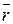 ,
, 

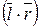 =
= 

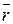 – ассоциативность.
– ассоциативность.
2.  +
+ 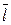 =
= 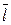 +
+  ,
, 

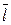 =
= 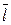

 – коммутативность.
– коммутативность.
3. Существует единственный нейтральный элемент:  +
+ 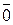 =
=  ,
, 

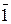 =
=  для "
для "  Î Z / m.
Î Z / m.
Пусть  – нейтральный элемент. Тогда
– нейтральный элемент. Тогда 
Пусть 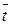 – нейтральный элемент. Тогда
– нейтральный элемент. Тогда 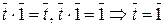 .
.
При m = 1 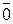 – также нейтральный элемент относительно умножения.
– также нейтральный элемент относительно умножения.
4. Для всякого  Î Z / m Z существует единственный противоположный класс
Î Z / m Z существует единственный противоположный класс 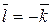 такой, что
такой, что  +
+ 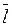 =
= 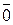 , при этом
, при этом 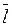 =
=  .
.
Пусть  . Тогда
. Тогда
 .
.
5.  – дистрибутивность умножения относительно сложения.
– дистрибутивность умножения относительно сложения.
Свойства 1, 2, 5 выполняются для всех 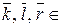 Z / m Z.
Z / m Z.
Определение 1.7.1. Элемент  Î Z / m Z называется обратимым, если найдется такой класс
Î Z / m Z называется обратимым, если найдется такой класс 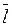 Î Z / m Z, что
Î Z / m Z, что 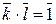 . Тогда
. Тогда 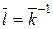 называют обратным классом к
называют обратным классом к  .
.
При m = 1  , Z / Z = {
, Z / Z = {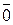 } и состоит из одного обратимого класса вычетов.
} и состоит из одного обратимого класса вычетов.
Из ассоциативности умножения вытекает, что если  – обратимый класс, то для него обратный класс определен однозначно.
– обратимый класс, то для него обратный класс определен однозначно.
Пусть  . Тогда
. Тогда
 .
.
Лемма 1.7.1. Пусть  Î Z / m Z – такой класс, что (k, m) = 1. Тогда
Î Z / m Z – такой класс, что (k, m) = 1. Тогда
1. для каждого 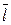 ¹
¹ 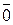
 ×
×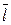 ¹
¹ 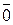 ;
;
2. 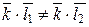 , если
, если  ;
;
3.  – обратимый класс в Z / m Z.
– обратимый класс в Z / m Z.
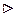
1. (k, m) = 1. Если бы $ l, 0 < l < m, такое, что  , то m | k × l, но по свойству 2 взаимной простоты m | l, что невозможно.
, то m | k × l, но по свойству 2 взаимной простоты m | l, что невозможно.
2. Если бы 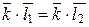 при
при  , то
, то  , то есть m | k × (l 1 – l 2), в силу свойства 2 взаимной простоты m | (l 1 – l 2), что невозможно, поскольку 0 < | l 1 – l 2 | < m.
, то есть m | k × (l 1 – l 2), в силу свойства 2 взаимной простоты m | (l 1 – l 2), что невозможно, поскольку 0 < | l 1 – l 2 | < m.
3. По критерию взаимной простоты (теорема 1.4.1) $ u, v Î Z такие, что k × u + m × v = 1 Þ 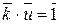 , то есть
, то есть 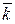 – обратимый класс,
– обратимый класс, 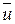 – обратный к нему класс.
– обратный к нему класс.
Лемма 1.7.2. Пусть  Î Z / m Z – такой класс, что (k, m) = d > 1. Тогда
Î Z / m Z – такой класс, что (k, m) = d > 1. Тогда
1. существует 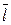 ¹
¹ 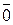 такой, что
такой, что  ×
×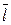 =
= 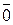 ;
;
2. существуют  такие, что
такие, что  ;
;
3. для всех 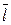 ¹
¹ 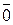
 ×
×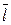 ¹
¹ 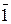 , то есть класс
, то есть класс  не обратим в Z / m Z.
не обратим в Z / m Z.
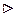
1. Так как (k, m) = d > 1, то m = d × l, где 1 < l < m, k = d × k 1, (k 1, l) = 1 по свойству 1 взаимно простых чисел. Тогда  , что означает
, что означает 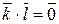 при
при 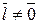 .
.
2. Существует 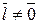 с условием
с условием 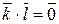 согласно утверждению 1 данной леммы. Рассмотрим
согласно утверждению 1 данной леммы. Рассмотрим  Î Z / m Z, построим класс
Î Z / m Z, построим класс 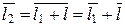 Î Z / m Z,
Î Z / m Z,  . Тогда
. Тогда 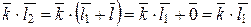 .
.
3. Если бы  был обратим в Z / m Z, то существовал бы
был обратим в Z / m Z, то существовал бы 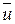 Î Z / m Z со свойством
Î Z / m Z со свойством 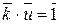 , то есть согласно условию 3 теоремы 1.6.1 k × u = 1 + m × q, q Î Z, Û k × u – m × q = 1 Û (k, m) = 1 (по критерию взаимной простоты), что не так.
, то есть согласно условию 3 теоремы 1.6.1 k × u = 1 + m × q, q Î Z, Û k × u – m × q = 1 Û (k, m) = 1 (по критерию взаимной простоты), что не так.
Из лемм 1.7.1 и 1.7.2 вытекает следующая теорема.
Теорема 1.7.1. Класс  Î Z / m Z обратим тогда и только тогда, когда (k, m) = 1. Произведение обратимых классов есть обратимый класс.
Î Z / m Z обратим тогда и только тогда, когда (k, m) = 1. Произведение обратимых классов есть обратимый класс.
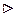 Первое утверждение следует из утверждений 3 лемм 1.7.1 и 1.7.2.
Первое утверждение следует из утверждений 3 лемм 1.7.1 и 1.7.2.
Пусть n ³ 2 и 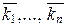 – обратимые классы,
– обратимые классы, 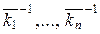 – соответственно обратные к ним классы. Тогда, поскольку операция умножения в Z / m Z коммутативна,
– соответственно обратные к ним классы. Тогда, поскольку операция умножения в Z / m Z коммутативна,
 .
.
Следовательно, 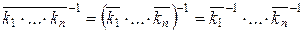 .
.
Следствие. Если p – простое число, то в Z / p Z каждый ненулевой класс обратим.
Поскольку Z / m Z состоит из конечного множества элементов, то сложение и умножение можно задавать поэлементно в виде таблиц. На пересечении i -й строки и j -го столбца таблицы пишется  (где
(где 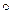 – знак операции). Так задавать алгебраические операции на конечном множестве впервые предложил известный английский математик XIX века Артур Кэли (1821–1895), поэтому такие таблицы называются таблицами Кэли.
– знак операции). Так задавать алгебраические операции на конечном множестве впервые предложил известный английский математик XIX века Артур Кэли (1821–1895), поэтому такие таблицы называются таблицами Кэли.
Пример 1.7.1. Построим таблицы сложения и умножения в Z /3 Z и в Z /4 Z – таблицы 1.7.1 и 1.7.2 соответственно – и найдем обратимые элементы.
Z /3 Z = 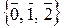 = {3 Z, 3 Z + 1, 3 Z + 2}.
= {3 Z, 3 Z + 1, 3 Z + 2}.
Таблицы 1.7.1
| + | 
| 
| 
| × | 
| 
| 
| |

| 
| 
| 
| 
| 
| 
| 
| |

| 
| 
| 
| 
| 
| 
| 
| |

| 
| 
| 
| 
| 
| 
| 
|
Из таблицы умножения 1.7.1 видно, что классы 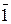 и
и 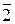 обратны сами себе.
обратны сами себе.
Z /4 Z =  = {4 Z, 4 Z + 1, 4 Z + 2, 4 Z + 3}.
= {4 Z, 4 Z + 1, 4 Z + 2, 4 Z + 3}.
Таблицы 1.7.2
| + | 
| 
| 
| 
| × | 
| 
| 
| 
| |

| 
| 
| 
| 
| 
| 
| 
| 
| 
| |

| 
| 
| 
| 
| 
| 
| 
| 
| 
| |

| 
| 
| 
| 
| 
| 
| 
| 
| 
| |

| 
| 
| 
| 
| 
| 
| 
| 
| 
|
Из таблицы умножения 1.7.2 видно, что классы 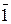 и
и 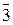 обратны сами себе, а класс
обратны сами себе, а класс 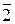 не обратим. ·
не обратим. ·
Определение 1.7.2. Функция Эйлера (или тотиент-функция) j ставит в соответствие каждому натуральному m > 1 количество натуральных чисел, меньших m и взаимно простых с m.
Эта функция обладает следующими свойствами.
Теорема 1.7.2 (о вычислении значений функции Эйлера).
1. j (p) = p – 1 для каждого простого числа p.
2. j (ps) = ps – ps – 1, "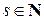 .
.
3. Если (n, m) = 1 то j (n × m) = j (n) × j (m).
4. Если  – каноническое разложение числа n, то
– каноническое разложение числа n, то
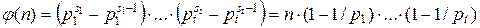 .
.
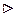
1. Количество чисел множества {1, 2, 3,…, p – 1}, взаимно простых с p, равно p – 1, так как любое число этого множества взаимно просто с p.
2. Рассмотрим множество
{1, 2, 3,…, p – 1, p, p + 1,…, 2 p,…, 3 p,…, 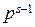 ,…,
,…, 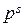 }.
}.
Разобьем это множество на подмножества {1, 2, 3,…, p – 1, p }, { p + 1,…, 2 p },…, { }. В каждом подмножестве число элементов, взаимно простых с p, равно p – 1. Всего таких подмножеств
}. В каждом подмножестве число элементов, взаимно простых с p, равно p – 1. Всего таких подмножеств 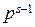 . Поэтому j (ps) = (p – 1) × ps – 1 = ps – ps – 1.
. Поэтому j (ps) = (p – 1) × ps – 1 = ps – ps – 1.
3. Рассмотрим множество {1, 2,…, n, n + 1,…, 2 n,…, (m – 1) n,…, mn }. Разобьем его на подмножества {1, 2, 3,…, n }, { n + 1, n + 2,…, 2 n }, {2 n + 1,…, 3 n },…, {(m – 2) n + 1,…, (m – 1) n }, {(m – 1) n + 1,…, (m – 1) n + n = mn }. В первом подмножестве количество чисел, взаимно простых с 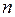 , равно j (n) по определению. Во всех подмножествах числа имеют вид
, равно j (n) по определению. Во всех подмножествах числа имеют вид 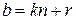 ,
,  , (b, n) = (n, r) (теорема 1.2.1), то есть количество чисел, взаимно простых с n, тоже равно j (n). Всего элементов, взаимно простых с n, в исходном множестве – j (n) × m. Числа, взаимно простые с m × n, взаимно просты с m и n одновременно. Пусть
, (b, n) = (n, r) (теорема 1.2.1), то есть количество чисел, взаимно простых с n, тоже равно j (n). Всего элементов, взаимно простых с n, в исходном множестве – j (n) × m. Числа, взаимно простые с m × n, взаимно просты с m и n одновременно. Пусть  – числа первого подмножества, взаимно простые с n. Тогда
– числа первого подмножества, взаимно простые с n. Тогда 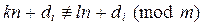 , 0 £ k, l £ m – 1, k ¹ l, так как
, 0 £ k, l £ m – 1, k ¹ l, так как  , ведь (n, m) = 1, 0 < | k – l | < m.
, ведь (n, m) = 1, 0 < | k – l | < m.
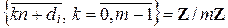 для фиксированного
для фиксированного 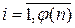 . Все множество чисел, взаимно простых с n, разобьем на j (n) подмножеств по m элементов в каждом, вычеты которых по модулю m все различны. В каждом множестве j (m) элементов, взаимно простых с m, так как их вычеты одинаковы в различных множествах, поэтому всего j (n) × j (m) элементов, взаимно простых с n и m одновременно.
. Все множество чисел, взаимно простых с n, разобьем на j (n) подмножеств по m элементов в каждом, вычеты которых по модулю m все различны. В каждом множестве j (m) элементов, взаимно простых с m, так как их вычеты одинаковы в различных множествах, поэтому всего j (n) × j (m) элементов, взаимно простых с n и m одновременно.
4. Пусть  – каноническое разложение числа n. Тогда
– каноническое разложение числа n. Тогда
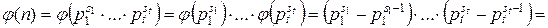
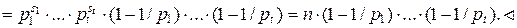
Пример 1.7.2. 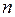 = 72 = 23 × 32.
= 72 = 23 × 32.
Следовательно, j (72) = (23 – 22) × (32 – 3) = 72 × (1 – 1/2) × (1 – 1/3) = 24. ·
Из теоремы 1.7.1 следует, что в Z / m Z имеется в точности j (m) обратимых классов.
Пример 1.7.3. j (18) = j (2 × 32) = 6, значит в Z /18 Z имеется в точности 6 обратимых элементов. Ими являются классы 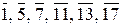 . ·
. ·
Теорема 1.7.3 (Л. Эйлер). Для " m Î N >1, a Î Z (a, m) = 1 тогда и только тогда, когда aj ( m ) º 1 (mod m).
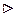 Необходимость. Если (a, m) = 1, то
Необходимость. Если (a, m) = 1, то 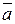 – обратимый элемент Z / m Z по теореме 1.7.1. Пусть
– обратимый элемент Z / m Z по теореме 1.7.1. Пусть  – все обратимые элементы в Z / m Z. Рассмотрим
– все обратимые элементы в Z / m Z. Рассмотрим
 .
.
Действительно, 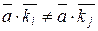 при i ¹ j по лемме 1.7.1, тогда
при i ¹ j по лемме 1.7.1, тогда 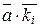 ,
, 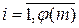 , – все различные обратимые классы по теореме 1.7.1. Следовательно,
, – все различные обратимые классы по теореме 1.7.1. Следовательно,

Так как 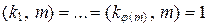 , то по свойству 6 сравнений aj ( m ) º 1 (mod m).
, то по свойству 6 сравнений aj ( m ) º 1 (mod m).
Достаточность. 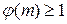 , aj ( m ) º 1 (mod m) Þ
, aj ( m ) º 1 (mod m) Þ 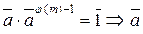 – обратимый элемент в Z / m Z Þ (a, m) = 1 (по теореме 1.7.1).
– обратимый элемент в Z / m Z Þ (a, m) = 1 (по теореме 1.7.1).
Следствие. В Z / m Z при m Î N >1 всякий обратимый элемент 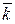 обладает свойствами: 1)
обладает свойствами: 1)  , 2) обратным к
, 2) обратным к 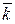 является класс
является класс 
Теорема 1.7.4 (малая теорема Ферма). Пусть p – простое число, a Î Z не делится на p тогда и только тогда, когда 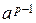
 1 (mod p).
1 (mod p).
Доказательство следует из теоремы Эйлера, поскольку j (p) = p – 1.
Следствие 1. В Z / p Z обратным к  ¹
¹ 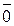 является класс
является класс 
Следствие 2. Если 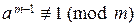 , m Î N >1, для некоторого целого a при (a, m) = 1, то m – составное число.
, m Î N >1, для некоторого целого a при (a, m) = 1, то m – составное число.
Этот факт часто используется для проверки числа на простоту. Он позволяет установить наличие нетривиальных множителей данного числа m, не находя ни одного из таких множителей.
|
|
|
|
Дата добавления: 2014-01-05; Просмотров: 1297; Нарушение авторских прав?; Мы поможем в написании вашей работы!