Геометрический смысл задачи линейного программирования

Рассмотрим следующую задачу линейного программирования:

, , .

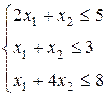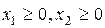Геометрическая интерпретация решения:

.

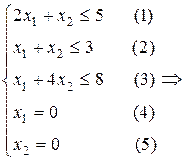
Нормальное уравнение прямой: ,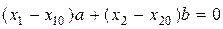

,

,

.

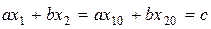Рис. 3.1. Геометрическая интерпретация решения экстремальной задачи

То есть наискорейшее возрастание функции F будет в направлении вектора . Координаты точки В удовлетворяют уравнению:

.

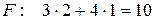Можно показать, что если задача линейного программирования имеет решение, то оно соответствует хотя бы одной угловой точке многогранника решений и совпадает, по крайней мере, с одним из допустимых базисных решений системы ограничений. Поэтому для решения задачи линейного программирования необходимо перебрать конечное число базисных решений, выбрать среди них то, на котором целевая функция принимает экстремальное значение. Геометрически это соответствует перебору всех угловых (крайних) точек многогранника. Если оптимальное решение существует, то такой перебор приведет к нахождению оптимального решения. Однако такой прямой перебор связан с очень большим объемом вычислений. Число перебираемых допустимых базисных решений можно сократить, если производить перебор не произвольно, а добиваясь того, чтобы каждое последующее решение было бы не хуже предыдущего. Такой подход, хотя и не исключает теоретической возможности перебора всех угловых точек, на практике позволяет существенно сократить число шагов при отыскании экстремума. Поясним это на графическом примере (см. рис. 3.2).

Пусть область допустимых решений изображается многоугольником ABCDEFGH. Пусть угловая точка B соответствует исходному допустимому базисному решению. При произвольном переборе всех вершин мы могли бы исследовать все семь вершин многогранника. В то же время видно, что после точки B выгоднее перейти к точке C, а затем к точке D, которая и будет оптимальной, т.е. вместо семи точек перебрали только три.

Идея последовательного улучшения решения легла в основу наиболее часто применяемого метода решения задач линейного программирования.

Рис.3.2. Область допустимых решений

Геометрический смысл симплексного метода состоит в том, что осуществляется последовательный переход от одной вершины многогранника ограничений к другой, соседней, в которой линейная функция принимает значение не худшее, чем в предыдущей. Эта процедура продолжается до тех пор, пока не будет найдено оптимальное решение. Симплексный метод, позволяющий решать любую задачу линейного программирования, универсален. В настоящее время он используется в программном обеспечении для решения задач линейного программирования на компьютере. Для решения задач небольшой размерности он может использоваться вручную.

Симплексный метод состоит из трех основных элементов:

1) определения какого-либо первоначального допустимого базисного решения;

2) правила перехода к лучшему решению;

3) проверки оптимальности допустимого решения.

Для использования симплексного метода задача линейного программирования должна быть приведена к каноническому виду, т.е. система ограничений должна быть представлена не в виде неравенств, а в виде уравнений.

Дата добавления: 2014-01-05