Система дифференциальных уравнений Навье - Стокса

Динамика реальной (вязкой жидкости)

При изучении движения реальной (вязкой жидкости) можно пойти двумя разными путями:

воспользоваться готовыми дифференциальными уравнениями и их решения­ми, полученными для идеальной жидкости. Учёт проявления вязких свойств осуществляется с помощью введения в уравнения дополнительных попра­вочных членов уравнения, вывести новые уравнения для вязкой жидкости.

Для практической инженерный деятельности более приемлемым следует считать первый полуэмпирический путь, второй следует использовать лишь в тех случаях, когда требуется детальное изучение процесса движения вязкой жидкости. По этой причине ог­раничимся лишь записью систем дифференциальных уравнений Навье - Стокса и поверх­ностным анализом этих уравнений.

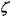При= const и= const система уравнений значительно упростятся:

Пренебрегая величинами вторых вязкостейи считая жидкость несжимаемой

(р = const), уравнения Навье - Стокса запишутся в следующем виде:

К уравнениям Навье - Стокса в качестве дополнительного уравнения принимается уравнение неразрывности. Учитывая громоздкость и трудность прямого решения задачи в практической деятельности (в случаях, когда это считается допустимым) решение дости­гается первым методом (по аналогии с движением идеальной жидкости).

5.2. Уравнение Бернулли для элементарной струйки вязкой жидкости

Выделим в элементарной струйке жидко­сти двумя сечениями 1 - 1 и 2 - 2 отсек жид­кости. Отсек жидкости находится под дейст­вием сил давленияи сил тяжести на жидкость в отсеке действуют также силы инерции самой движущейся жидкости, а также силы трения, препятствующие перемещению 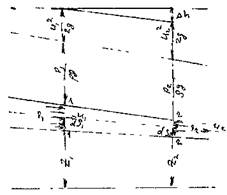жидкости. В результате действия сил внутрен­него трения часть механической энергии жид­кости расходуется на преодоление возникающих сопротивлений. По этой причине вели­чины гидродинамических напоров в сечениях будут неодинаковы. Естественно, что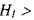//2.Тогда разность гидродинамических напоров в крайних сечениях отсековбудут как раз характеризовать потери напора на преодоление сил трения. Эта величина носит название потерь напора на трение

В этом случае уравнение Бернулли примет следующий вид:

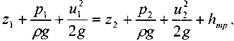
- потери удельной энергии (преобразование потенциальнойэнергии жидкости в тепловую энергию при трении).

Величинаносит название гидравлического уклона.

Дата добавления: 2014-01-05