Determinants

Дросселирование.

При встрече потока с сужением (вентиль, капилляр, мембрана с малым отверстием на оси и т.п.) потери на трение максимальны. Работа трения переходит в теплоту и вся эта теплота остается в потоке. Поэтому такой процесс (его называют дросселированием или мятием) имеет инвариант h = const. Наверное, понятно из рис. 5.14 (см. процесс 1 – 4 (пунктир)), что при дросселировании давление уменьшается (dp < 0), удельный объем вещества в потоке соответственно растет (dv > 0), энтропия обязательно увеличивается (ds > 0). А вот об изменении температуры потока поговорим в лекции 7.

Пример 4. Пар движется по конфузору в условиях примера 3, но с трением при известном коэффициенте скорости φ = 0,93. Найти реальную скорость пара на выходе из конфузора.

Решение. Потери энтальпии на трение рассчитываются по формуле (5.18):

Δ_трения = (h₁ – h_k)(1 – φ²) = (3128 – 2944)(1 – 0,93²) = 25 кДж/кг.

Величина энтальпии пара на выходе из конфузора (точка 3 на рис. 5.14) равна:

h_трения = h_k + Δ_трения = 2944 + 25 = 2969 кДж/кг.

Реальная скорость истечения пара из конфузора:

w₃ = [2(3128 – 2969)10³]^1/2 = 564 м/с (а было w₂ = 607 м/с).

Ответ: скорость истечения пара из конфузора w₃ = 564 м/с.

Пример 5. В цехе химического завода со взрывоопасными условиями работы приводом для компрессора является паровая турбина с питанием перегретым паром с давлением р = 5 бар, а заводская котельная производит пар с давлением 15 бар и температурой 240⁰С. Как трансформировать котельный пар и сделать его пригодным для паровой турбины?

Решение. Один из способов трансформации (не единственный) – подвергнуть пар из котельной мятию (дросселированию) (см. рис. 5.14, процесс 1 – 4).

По диаграмме h – s для водяного пара находим параметры состояния в точке 1. Сама точка 1 находится на пересечении изобары р₁ = 15 бар и изотермы Т₁ = 240⁰С. Считываем с диаграммы для точки 1 величину энтальпии h₁ = 2898 кДж/кг.

Точка 4 (см. рис. 5.14) находится на пересечении линии h = const = 2898 кДж/кг и изобары р₂ = 5 бар. Опять с диаграммы считываем величину температуры Т₂ = 225⁰С.

Ответ: можно применить процесс дросселирования до давления р₂ = 5 бар. Получится перегретый пар, пригодный для питания турбины.

Замечание. Конечно, такое решение проблемы обрадует заводчан своей простотой и отсутствием специальной обслуги «трансформации» пара. Но решение очень не экономичное: из хорошего и дорогого пара сделали пар с большой энтропией, себестоимость целевого продукта химического завода такое решение только увеличит.

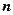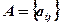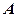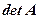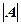Definition 3.1: Each - square matrix is assigned a special scalar called the determinate of, denoted by or, or

.

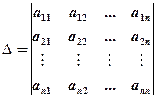Determinant of order 1: ;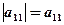

Determinant of order 2: ;

Determinant of order 3: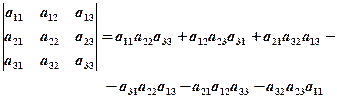

Definition 3.2: Minor of an element of determinant 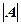is a determinantobtained from determinant 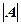deleting its -th row and 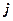-th column and denoted.

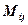Definition 3.3: A quantity 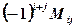is called cofactor of an element of determinant 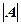and denoted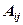

.

Theorem (Laplace expansions): The determinant of a square matrix 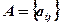is equal to the sum of the products obtained by multiplying the elements of any row (column) by their respective cofactors

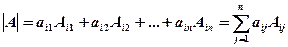
§4. Solution of system of 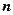linear equations in 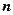unknowns.

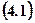
The system 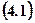is a system of 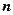linear equations in 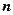unknowns. 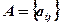– is a matrix of the coefficients of unknowns of system, 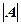– is a determinant of this matrix, 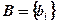– matrix -column of constant terms.

1. Cramer’s method.

Theorem 4.1: If 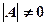, the system 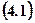has unique solution, which is defined by the formulas:

, , …, ,

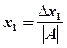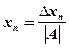where determinants 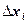are received from 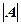by replacing the -th column of 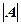by the column of constant terms.

Дата добавления: 2014-01-05