Система двух линейных уравнений с двумя неизвестными

БЛОК

Лекториум
(продолжительность 2-3 часа)

1. Лекции (для мужчин и женщин)

Это по-настоящему волшебный авторский курс лекций для женщин, слушая который можно в корне положительно изменить свою жизнь: достичь уверенности, самосовершенствования и познания (самоисцеления, самоощущения и т.п.).

Темы лекций (могут корректироваться):

1. Секреты сохранения женского здоровья

2. Способы самоисцеления

3. Дружба: миф или реальность?

4. Энергия любви — что с ней делать?

5. Подготовка ко встрече с «единственным»

6. Мир желаний — какой он?

Результат:

расширение знаний о психологии мужчин и женщин, их поведения в различных ситуациях,осознание своих деструктивных шаблонов поведения (в быту, в семье), знакомство с конструктивными навыками в поведении с противоположным полом.

Стоимость: от 300 руб./чел. (обговаривается с организатором)

Необходимые материалы: удобные места для сидения, доска с мелом или ватман с маркерами, питьевая вода + стаканчики, салфетки.

Ведущий: Анна Благова

2. Общая лекция по су-джок терапии:

Су-Джок терапия (в пер. с корейского Су – кисть, Джок – стопа) — это метод лечения с использованием кистей и стоп. В строении кисти и стопы проявляется удивительное подобие строению человеческого тела.

С древнейших времен человечество владело знанием о том, что отдельные участки нашего тела взаимодействуют с другими участками тела и со всем организмом, и использовало это в целях диагностики и лечения болезней с помощью иглоукалывания, точечного массажа, прогревания и т.д.

Так, Су Джок терапия сфокусирована на использовании кистей и стоп в качестве инструмента исцеления всего организма. На общей лекции мы будем осваивать базовые элементы этой методики.

Результат:

- знакомство с семью самыми главными "реанимационными" точками

- основы семянотерапии (лечение любых заболеваний) с помощью семян овса, пшеницы, ржи и т.п.

- определение заболеваний на стадии их зарождения (то, что узи еще не показывает)

- полная диагностика каждому участнику + программа по индивидуальному лечению

Стоимость: от 300 руб./чел. (обговаривается с организатором)

Необходимые материалы: удобные места для сидения, доска или ватманы и маркер, тетради, питьевая вода + стаканчики, салфетки.

Ведущий: Анна Благова

Запишем линейную систему двух уравнений с двумя неизвестными в следующем виде:

a₁ x + b₁ у = c₁ a2 x + b2 y = C2

Чтобы решить эту систему, умножим первое уравнение на b₂, второе - на (- b₁) и сложим их; в результате получим уравнение:

x(a^ - a2b1) = - C2b1 (4)

Аналогично, умножая первое уравнение на (- a₂), второе - на a₁, получим уравнение:

У(aA - a2b1) = a1C2 - a2c (5)

Введем три определителя второго порядка

А:

a₁ b₁

^a2 ^b2

a₁b₂ - a₂b₁; А₁

^c1 ^b1 C2 b2

C1b2 - C2b1 ^; А2

a₁ C₁

^a2 ^C2

^a1 ^C2 ^{- a}2^C1

Определитель А называется определителем системы (3). Уравнения (4) и (5) дают систему уравнений, эквивалентную системе (3):

Ax = А₁, Ау = А ₂

(6)

Для решения системы (6) рассмотрим три случая:

1) А ф 0. Следовательно:

x= —, y = —

АА

Формулы (7) дают единственное решение линейной системы (3) и носят название формул Крамера для решения системы двух линейных уравнений с двумя неизвестными.

2) А = О, А₁ = О, А₂ = 0. В этом случае система (6), а, следовательно, и система (3) имеет бесчисленное множество решений. Для нахождения этих решений достаточно заметить, что из условий А = А₁ = А ₂ = 0 вытекает

пропорциональность соответствующих коэффициентов и свободных членов уравнений системы (3), то есть

a₂ = Aa₁, b₂ = ЛЬ₁, c₂ = Ле₁

Таким образом убеждаемся, что система (3) эквивалентно одному уравне­нию:

a₁ x + b₁ y = c₁

Для решения этого уравнения положим, например, x = t, где t - произ­вольное вещественное число; тогда при b₁ ф 0 получим:

c₁ - a₁t

^y

Если же b₁ = 0, то получаем y = t, тогда x

a₁

3) А = 0, А₁ ф 0 (или А₂ ф 0). Система (6), а, следовательно, и система (3)

несовместна.

Пример. Решить системы уравнений:

а) \ б) \ в) \ ^У

|3x + y = -1 [4x - 6y = 2 [4x - 6y = -1

Решение. Вычислим определители А, А₁, А₂:

а) А:

25 31

-13, А1

85 -1 1

=13, А₂

2 8

3 -1

-26.

гая y = t, получим x

где t - произвольное вещественное число. В ча-

a₁ x + b₁ y + c₁ z = d₁ a₂ x + b₂ y + c₂ z = d₂ a₃ x + b₃ y + c₃ z = d₃

Чтобы найти решение системы (8) введем четыре определителя третьего порядка:

А1

x = —

А

у-

А2

А

_z=А3

^Z А

(14)

Формулы (14) называются формулами Крамера для решения системы трех линейных уравнений с тремя неизвестными.

При А = 0 и хотя бы одном из А₁,А₂,А₃, отличном от нуля, система (13), а потому и система (8), несовместна.

2x- 3y+ 2z =1, x- y- +z = 2, x- 2y+ z = -1.

Примеры. Решить системы уравнений: Гx + 2y + 3z = 7, Г2x - 3y + 2z = 1,

1)

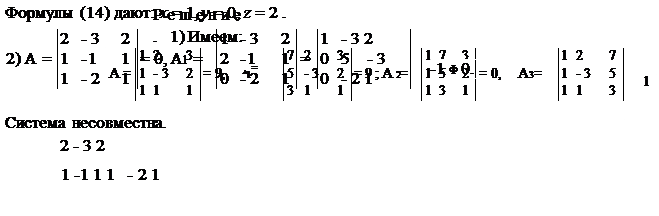x - 3y + 2z = 5, 2k x - y -+ z = 2, 3)<j x + y + z = 3. I x - 2y + z = 0.

3) А

0,

		-3										-3
^А1 ^=		-1		= 0,	^А2 ^=				= 0,	^А3 ^=		-1		= 0.
	-1	-2					-1					-2	-1

Система имеет бесчисленное количество решений. Заметим, что третье уравнение этой системы есть следствие первых двух уравнений (разность первого и второго уравнений). Следовательно, система эквивалентна системе двух линейных уравнений с тремя неизвестными:

^r2x - 3y + 2z = 1, x - y + z = 2.

Полагая z = t, x и y найдем из системы:

2 x - 3 y = 1 - 2t

x- y= 2 - t

x = 5 -1, y = 3. Итак, получим множество решений: x = 5 -1, y = 3, z = t, где t -

произвольное вещественное число.

1. Действия над матрицами.

Множество чисел, расположенных в виде прямоугольной таблицы

^а21 ^а22

^а2п

(1)

^ат1 ^ат2

имеющей т строк и п столбцов, называется прямоугольной матрицей размера т х п.

Числа, составляющие матрицу (1), могут быть как комплексными, так и вещественными и называются ее элементами.

Матрица называется в е щ е с т в е н н о й, если все ее элементы -вещественные числа.

Мы будем рассматривать, как правило, вещественные матрицы.

Если т=п, то матрица (1) называется к в а др а т н о й матрицей порядка п.

Например, матрица

(2 1 0^

J

имеет размер 2 х 3, а матрица

(2 3 ^

I-1 0 J

является квадратной матрицей порядка 2.

Квадратная матрица, у которой все элементы, расположенные вне г л а в н о й диагонали, идущей с левого верхнего угла в правый нижний, равны нулю, называется д и а г о н а л ь н о й матрицей.

Диагональная матрица имеет вид

'а_п 0 0...0^

^{0 а}22 ^{... 0} , 0 0... j

У диагональной матрицы все элементы с неравными индексами равны нулю, то есть =0, если i=j.

Диагональная матрица

1 0 0 1

0 ^

называется единичной матрицей и обозначается буквой Е

Матрица, все элементы которой равны нулю, называется н у л е в о й матрицей и обозначается буквой О.

Наряду с записью матрицы в виде (1) будем употреблять и сокращенную запись: (а у< i < m,1 < j < n).

Для обозначения матриц будем использовать также прописные буквы латинского алфавита A, B, C,..., X,Y,....

Матрица A= (а₁,а₂,...,а₃), состоящая из одной строки, называется

с т р о ч н о й матрицей длины n или в е к т о р - с т р о к о й; матрица

B

^f в1 ^Л

в2

состоящая из одного столбца, называется с т о л б ц о в о й матрицей высоты m или в е к т о р - с т о л б ц о м.

Пусть A_i = (а_п,а^,...,а_п) - i-ая строка матрицы (1), (i=1,2,...,m), bj,

(j=1,2,_,n), - j-ый столбец матрицы (1). Иногда бывает удобным записывать матрицу (1) в виде столбца ее строк или в виде строки ее столбцов:

А2

Сложение матриц и умножение матрицы на число Определение. Две матрицы А и В называются равными, если они имеют один и тот же размер и все их соответствующие элементы равны, то есть если А=) и В=(), (i=l,2,...,m, j=l,2,...,n), то А=Во ау = ву для всех

указанных i и j.

Определени е. Суммой двух матриц А и В одного и того же размера называется матрица С=А+В того же размера, элементы которой равны суммам соответствующих элементов данных матриц, то есть если А = (а_ц), В=()и С=(сф, то су=ау+ву,^=1,2,...т, j=1,2,...n).

Операция вычисления суммы матриц называется сложением матриц. Справедливо очевидное равенство: А+О=А. Пример. Пусть

	f з				f о
А=				, В=
	V1		^2 у		V^- ^4		^0 у

Тогда

f 3 7 3 ^л

С=А+В= 5 12 13

- 3 9 2

V У

Правило сложения двух матриц обобщается на случай любого конечного числа слагаемых матриц.

Из определения сложения матриц непосредственно следует, что эта операция коммутативна и ассоциативна, то есть

А+ В=В+А, (А+В)+С=А+(В+С).

Определение. Произведением матрицы А=(аф на число а (вещественное или комплексное) называется матрица а А, элементы которой есть элементы матрицы А, умноженные на а, то есть

аА = (аау < i < m,1 < j < n).

Пример.

4 У

'15 10 35^ _v40 5 20У

Операция умножения матрицы на число обладает следующими свойствами

а(А + В) = аА + аВ,

(а + в) А = аА + /ЗА,

(ар) А = а(/А).

Разность двух матриц А и В одного и того размера определяется равенством

А-В=А+(-1)В.

Произведение матриц

Определение. Произведением матрицы А=(аф размера тхn на матрицу В=(вф размера n хp называется матрица С=АВ=(сф размера т хp, где

n

^сЧ= Z ^aik^bkj = ^ai1^b1 j + ^ai 2^b2 j + ^... + ^ain^bnj k=1

(i=1,2,...rn, j=1,2,...n). Согласно этому определению, произведение двух матриц имеет смысл только тогда, когда число столбцов первой матрицы равно числу строк второй матрицы. Отсюда, квадратные матрицы одного и того же порядка всегда можно перемножить.

В общем случае умножение двух матриц зависит от порядка сомножителей, то есть оно некоммутативно: АВ ф ВА, (или даже ВА не имеет смысла).

Произведение трех матриц (если оно имеет смысл) ассоциативно, то есть

АВС=А(ВС)=(АВ)С.

Отметим легко проверяемое тождество:

АЕ=ЕА=А,

справедливое для любой квадратной матрицы А и единичной матрицы Е того же размера, что и матрица А. Примеры.

^f2 4Y5 1 ^ f2 ■ 5 + 4 ■ 2 2 ■ 1 + 4 ■ 3^ f 18 14^

3 ■ 5 + 5 ■ 2 3 ■ 1 + 5 ■ 3 у

25 18

f2

v¹

4 2

3 ^

f 1 2^

V2

' 2 ■ 1 + 4 ■ 3 + 3 ■ 2 2 ■ 2 + 4 ■ 1 + 3 ■ Л _v1 ■ 1 + 2 ■ 3 + 3 ■ 2 1 ■ 2 + 2 ■ 1 + 3 ■ 1

f 20 1Г|

13 7

Отметим некоторые полезные свойства умножения матриц. Пусть Ву обозначает j-ый столбец матрицы В, а A_i означает i-ую строку матрицы А. Тогда справедливы формулы:

f А₁В ^

АВ = (АВ1, АВ2,..., АВ p)

^А2^В

{a_iB_j = 1,2,...,т, j = 1,2,...,p). (2)

V ^Ат ^В У

2. Обратная матрица. Матричная запись системы линейных уравнений и ее

решения.

Определение. Квадратная матрица А называется невырожденной, если ее определитель не равен нулю, то есть detA ф 0.

Если же detA=0, то матрица А называется вырожденной.

Определение. Матрица А'¹ называется обратной матрице А, если АА^-1=А^-1А=Е. (4)

Теорема. Всякая невырожденная матрица А имеет единственную обратную матрицу А^-1, причем

а^-1=А

А

^А11 ^А21 ^А12 ^А22

V^A1n ^A2n

_А

^An 2

^Ann

(5)

где Aj - алгебраическое дополнение элемента а у, (1 < i < n,1 < j < n), матрицы A.

Отметим, что если А - невырожденная матрица, то и обратная ей матрица А^-1 так же - невырожденная, причем справедлива равенство

(А^-1)^-1=А.

Укажем без доказательства следующую теорему.

Теорема. Произведение АВ невырожденных матриц А и В является невырожденной матрицей, при этом

(АВ)'¹=В'¹А^-1. Пример. Найти обратную матрицу для матрицы

(2 -1 0 ^Л

А =5 3 - 6

_V-1 - 2 3

^А13

Следовательно,

-1 1 2

f- 3 3 6

f

-1

2 5

4 11 3 У

А

9 6 7 5

Матричные уравнения Пусть А - заданная невырожденная матрица порядка п, В и С - заданные прямоугольные матрицы размеров соответсвенно п х р и р х п. Требуется найти

неизвестные матрицы Хи У, удовлетворяющие уравнениям:

1) АХ=В, 2) УА=С. Умножив первое уравнение слева на А^-1, второе - справа на А'¹, получим:

Х=А^-1В, У=СА^-1.

При р=1 матричное уравнение 1) представляет собой систему (1), в которой положено т=п; при этом равенство Х=А^-1В называется правилом Крамера в матричной форме.

Пример. Решить систему уравнений матричным способом:

х1 + 2 х2 + — 2, 2 х1 + 2 х3 — 6,

х1 + х2 + х3 — 2.

2 -6 V ² У

Запишем эту систему в матричной форме:

^ f о Л

х

f1

23 32 11

Находим: detA=10, то есть матрица системы невырожденная. Поэтому

^f-5 1 13 ^

А"¹ =

0 5

24 17

Откуда

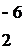
f 1 1

2,

то есть х₁=1,х₂=2,х₃=-1

Дата добавления: 2014-01-05