Одновременность существования свойств

Эквисатисные свойства, составляющие группу свойств, должны быть такими, чтобы оцениваемый объект в каждый момент времени мог одновременно обладать всеми этими свойствами. Соответственно и признак деле­ния должен выбираться с учетом удовлетворения этому правилу.

Например, во фрагменте дерева, приведенном на рис. 4.13, это правило нарушено: понятно, что восстановленная деталь не мо­жет быть одновременно покрыта хромом, медью, цинком. А это означает, что признак деления здесь выбран неправильно.

Сходный по характеру, но уже правильный пример деления на группу эквисатисных свойств приведен на рис.4.14 - здесь все свойства, составляющие группу, могут существовать одно­временно. Таким образом, кроме того, что признак деления должен быть единым, он еще выбирается так, чтобы обеспечить одновременное существование свойств в группе.

	Хром
Покрытие детали	Медь
	Цинк

Рис 4.13. Пример неправильного выбора признака деления – свойства, включенные в группу, не могут существовать (т.е. быть присущи объекту) одновременно

Качество покрытия деталей, нанесенных на участке гальванопокрытий	Качество покрытий поршневого пальца
Качество покрытия стержня клапана
	Качество покрытия толкателя клапана

Рис.4.14. Пример правильного выбора признака деления - свойства, включенные в группу, могут сущест­вовать (т.е. быть присущи объекту) одновременно

19. Предпочтительность признака де­ления меньшей размерности.

Совершенно очевидно, что из двух деревьев, имеющих на последнем уровне одинаковые свойства, более предпочтительным, при прочих равных условиях, является дерево, содержа­щее на предыдущих уровнях меньшее число сложных свойств, так как при этом уменьшаются затраты труда и времени на работу с деревом.

Разумеется, это правило должно применяться только в случаях, когда оно не противоречит другим пра­вилам построения дерева (например, правилу о возмож­ности использования поддеревьев).

Работоспособность грузового автомобиля	В дорожных условиях I категории	Летний сезон
Зимний сезон
В дорожных условиях II категории
Летний сезон
Зимний сезон
В дорожных условиях III категории
Летний сезон
Зимний сезон

Рис.4.15. Фрагмент дерева свойств с использованием признака деления, имеющего 3 градации, а потом 2 градации.

Степень детализации дерева в обоих случаях одинакова, но во втором случае (рис.4.15) фрагмент дерева состоит из девяти свойств против десяти в первом случае (рис.4.16.). Понятно, что при прочих равных условиях более предпочтительным является дерево, содержащее меньшее число элементов, чем и объясняется существование этого правила.

Работоспособность грузового автомобиля	Летний сезон	В дорожных условиях I категории
В дорожных условиях II категории
Зимний сезон	В дорожных условиях III категории
В дорожных условиях I категории
В дорожных условиях II категории
	В дорожных условиях III категории

Рис.4.16. Фрагмент дерева свойств с использованием признака деления, имеющего 2 градации, а потом 3 градации.

20. Минимум свойств в группе.

В литературе встречаются рекомендации, касающиеся только максимально допустимой ширины группы свойств. Так, существуют работы, которые рекомендуют принимать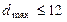, а в известной системе ПАТТЕРН принималось .

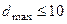Что же касается оптимальной ширины группы d _{o р t}, то соответствующих данных в литературе нет. Психологические возможности человека (и, разумеется, экс­перта) таковы, что при использовании большинства разновид­ностей экспертного метода ему трудно (практически невозможно) одновременно учитывать больше семи различных свойств, характеризующих какой-либо объект (например, семь свойств, образующих группу и характеризующих соответствующее сложное свойство).

Существует гипотеза, подтверждённая экспериментом, что погрешность коллективной экспертной оценки есть моно­тонно возрастающая функция от ширины группы. Из этого следует, что при пост­роении дерева желательно стремиться к минимальной ширине каждой группы (в случае если коэффициенты весо­мости будут определяться экспертным методом), т. е. d _{o р t} =2 и d _{o р t}= 7.

Общая же тенденция такова - чем меньше свойств в группе, тем легче работать эксперту и тем точнее выносимое им суждение. В идеале в каждой группе желательно было бы иметь два свойства: точность оценки эксперта при этом будет максимально высокой.

С этой точки зрения фрагмент дерева, изображенный на рис.10.5., целесообразно трансформировать так, чтобы путем введения в дерево еще одного уровня обеспечить нахождение в каждой группе не более двух свойств. Характер вносимых с этой целью корректировок легко понять, если сравнить рис. 4.5. с рис.4. 17..

Внутренние размеры кузова рефрижератора		Длина кузова
Площадь кузова
		Ширина кузова
Высота кузова

Рис.4.17. Пример построения фрагмента дерева с минимальным числом свойств в группе

21. Ясность признака деления.

Если по ситуации оценки установлено, что коэффициенты весомости для свойств отдельных групп (или для всего дерева в целом) будут определяться экспертным методом, целе­сообразно, чтобы в каждой группе свойств признак деле­ния был четко выражен и абсолютно ясен уже из самих формулировок свойств. В этом случае, как показывает практический опыт проведения экспертных опросов, экс­перты дают, при прочих равных условиях, более уверен­ные и точные ответы на поставленные им вопросы.

22. Однозначность толкования форму­лировок свойств.

Представляется достаточно оче­видным, что в дереве как одном из инструментов приня­тия решения не должны быть нечеткие, двусмысленные, неоднозначно трактуемые формулировки свойств. В про­тивном случае в принимаемые решения может быть вне­сена дополнительная погрешность. Крат­кое название свойства позволяет разным специалистам вкладывать в него различное содержание.

Дата добавления: 2014-01-05