План лекции. Решение задач математической логики

Решение задач математической логики

Лекция №5

1. Упрощение логических функций, заданных
в различной форме

2. Вычисление значения логического выражения
для заданных наборов переменных

3. Построение таблиц истинности булевых
функций

4. Определение тождественности булевых
выражений

1. Упрощение логических функций, заданных
в различной форме

Задача 1.

Упростить логическую функцию, заданную выражением

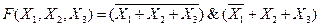
Задача упрощения функции сводится к тому, что исходное выражение надо преобразовать к более простому, сокращенному виду (минимизировать выражение по количеству входящих в него переменных и по количеству операций, которые присутствуют в этом выражении).

Речь идет о количестве вхождений каждой переменной. Каждая может входить несколько раз, и чем меньше она входит, тем более оптимальная считается функция по этому критерию.

Решение:

Шаг 1.
Первым делом избавимся от инверсии, которая охватывает длинную дизъюнкцию в первой скобке. Для этого используем закон де Моргана:

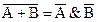
Инверсия дизъюнкций есть конъюнкция инверсий.

Получаем:

­

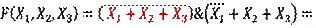
Первая скобочка – есть инверсия дизъюнкций, мы приводим ее к конъюнкции инверсий. Таким образом, у нас получается более упрощенное выражение. Но самое главное – избавление от длинной инверсии.

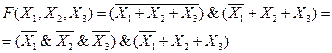
Шаг 2.
Теперь раскроем скобки, используя дистрибутивный закон:

Дистрибутивность умножения относительно сложения

А & (В ÚС) = (А & В)Ú (А& С)

Получаем:

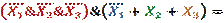
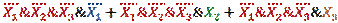
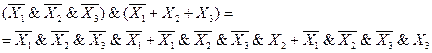
Шаг 3.
Упростим каждую элементарную конъюнкцию, используя законы:

а) противоречия А& Ā = 0

б) идемпотентности А& А = А

На третьем шаге нужно рассмотреть каждую конъюнкцию и постараться проанализировать, можно ли использовать вышеприведенные законы.

Получаем:

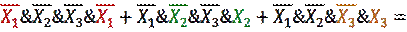
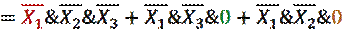
Шаг 4.
Наконец, используем законы логического умножения на константу 0:

А & 0 = 0

и логического сложения с константой 0:

А + 0 = A

Получаем:

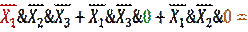
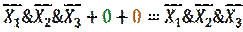
Таким образом,

Ответ:

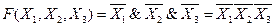
В итоге видно, что мы существенно упростили формулу.

Задача 2.

Упростить логическую функцию, заданную выражением

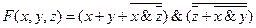
Решение:

Шаг 1.
Первым делом избавимся от «длинных» инверсий, используя законы де Моргана

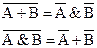
Инверсия дизъюнкций есть конъюнкция инверсий.

Инверсия конъюнкция есть дизъюнкция инверсий.

Получаем:

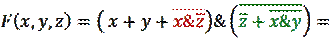
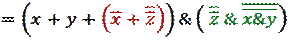
Красным выделено первое преобразование, зеленым – второе.

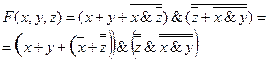
Шаг 2.
Теперь используем законы двойного отрицания и ассоциативности (уберем внутренние скобки)

Получаем:

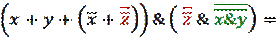
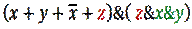
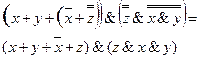
Шаг 3.
Теперь для первой скобки используем закон исключенного Третьего

A + Ā = 1

Дизъюнкция А и не А есть всегда 1. Или событие, или его отрицание должно произойти (или на улице идет дождь, или не идет).

Получаем:

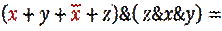
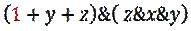
Далее используем законы:

а) с константой «1»: 1 + A = 1

б) ассоциативный (от изменения мест
переменных конъюнкция не меняется)

Ответ:

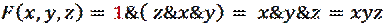
Задача 3.

Упростить логическую функцию F (x, y, z), заданную таблично. Значение функции равно 1 на наборах 000, 001, 010, 011, 111.

x	y	z	F

Решение:

Шаг 1.

Построим СДНФ.

Для этого необходимо единичные наборы преобразовать к набору переменных.

Если значение равно нулю – элемент конъюнкции с инверсией. Если один – без инверсии.

Единичные наборы:

000 001 010 011 111

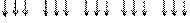
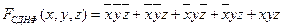
Пишем набор по единичным наборам.

Вместо двоичных значений в таблице мог быть набор в десятичной форме:

0, 1, 2, 3, 7.

Теперь Преобразуем СДНФ к более компактному виду.

2. Добавим еще одну конъюнкцию, используя закон A+A=A:

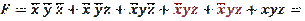
3. Группируем по две конъюнкции и далее используем правило склеивания:

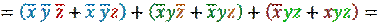
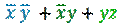
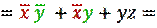
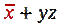
Преобразуем СДНФ к более компактному виду.

Дата добавления: 2014-01-05