События и их виды

ОСНОВНЫЕ ПОНЯТИЯ И ТЕОРЕМЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ.

ЛЕКЦИЯ 1

Теория вероятностей — математическая наука, изучающая количественные закономерности массовых случайных явлений.

Случайным называют такое явление, которое при неоднократном воспроизведении одного и того же опыта протекает каждый раз несколько по-иному.

Всякое осуществление определённых условий и действий, при которых наблюдается изучаемое явление, называют опытом.

Любая качественная характеристика опыта называется событием. Например, при стрельбе по мишени могут происходить два события: попадание в мишень и промах.

Количественная характеристика опыта называется случайной величиной. Примерами случайных величин могут служить результаты измерений некоторой величины, координаты точек попадания при выстрелах и т.д.

При выполнении определённого комплекса условий различают события: достоверные, невозможные и случайные.

Достоверным называют событие, которое обязательно произойдёт, например, событие появления белого шара при взятии одного шара из урны, содержащей только белые шары.

Невозможным называют событие, которое никогда не происходит, например, событие появления чёрного шара при взятии одного шара из урны с белыми шарами.

Случайным называют событие, которое при осуществлении определённого комплекса условий может или произойти, или не произойти. Например, при бросании монеты она может упасть кверху либо гербом, либо цифрой. События: "выпадение герба", "выпадение цифры" — случайные события.

События обычно обозначают заглавными буквами начала латинского алфавита: 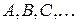или .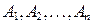

Виды случайных событий:

§ совместные — события, которые при испытании могут происходить одновременно (например, попадание в цель и разрыв снаряда — события совместные);

§ несовместные — события, которые не могут произойти вместе (например, появление герба и цифры при одном бросании монеты);

§ равновозможные — события, имеющие одинаковую объективную возможность появления (например, выпадение герба и выпадение цифры при бросании монеты — события равновозможные);

§ полная группа событий — такие события, одно из которых обязательно произойдёт при выполнении определённого комплекса условий (например, события выпадения граней с цифрами 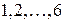образуют полную группу, так как в результате бросания игральной кости одно из них обязательно произойдёт);

§ противоположные — два несовместных события, образующих полную группу (событие, противоположное событию А, обозначают через , например, А — событие "попадание при выстреле", — "промах при выстреле");

§ независимые — события, имеющие возможность появления, не зависящую от того, появились или не появились другие события (например, событие "выпадение герба" на первой монете не зависит от того, какая сторона монеты выпала на второй монете, если опыт состоит в одновременном подбрасывании двух монет);

§ зависимые — события, у которых возможность появления зависит от того, произошли или не произошли другие события (например, если поражение цели достигается двумя попаданиями, то поражение цели при втором выстреле есть событие зависимое, так как оно может произойти лишь при условии первого попадания в цель).

С каждым событием связывают определённое число, называемое вероятностью. Вероятность — численная мера степени объективной возможности появления события. Если достоверному событию приписать вероятность, равную единице, а невозможному событию — вероятность, равную нулю, то диапазон изменения вероятностей любых событий будет определяться выражением

.

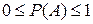1.2 НЕПОСРЕДСТВЕННЫЙ ПОДСЧЁТ ВЕРОЯТНОСТЕЙ

Существуют события, вероятности которых можно определить из условий самого опыта, не производя его. Для этого необходимо, чтобы элементарные события, составляющие полную группу, были попарно несовместными и равновозможными. Для таких событий возможен непосредственный подсчёт вероятностей, основанный на оценке доли "благоприятных" случаев.

Вероятность события вычисляют по формуле, называемой " формулой непосредственного подсчёта вероятностей "

.

где N — общее число случаев, М — число случаев, благоприятствующих появлению события А.

Формулу называют также классическим определением вероятности.

Так, найдём вероятность события появления герба при одном бросании монеты:

.

Задача 1.1. В ящике находится 10 бракованных и 15 стандартных изделий. Найти вероятность того, что извлечённая наугад деталь будет стандартной.

Решение. Общее число случаев — ; число случаев, благоприятствующих появлению стандартной детали — . Искомая вероятность равна

.

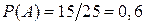Дата добавления: 2014-01-05