Интеграл вероятностей

Более удобной для табулирования является функция 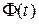, называемая интегралом вероятностей

.

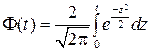Численно функция 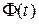равна заштрихованной площади на рис. 3.3. (в осях t и ).

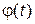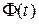— функция нечётная, т.е. 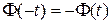, что позволяет объём таблиц для неё сократить вдвое по сравнению с таблицами для . В Приложении B приводится таблица значений функции .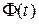

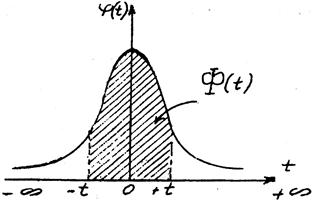
Рис. 3.3 — Интеграл вероятностей

По графикам, представленным на рис. 3.2 и рис.3.3, можно установить соотношение между и 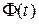. Согласно 2‑му свойству плотности вся площадь под кривой распределения равна единице. Заштрихованную на рис. 3.2 площадь, численно равную , разобьём на две части (от 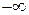до 0 и от 0 до t), одна из которых равна 0,5, а вторая — . Получаем формулу связи функции распределения и интеграла вероятностей

.

Формула с учётом примет вид:

.

Известно также, что функция 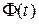представляет собой вероятность попадания случайной величины Х в интервал, симметричный относительно математического ожидания (в осях х и 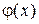), т.е.

.

Для случайных ошибок измерений выражение примет вид:

.

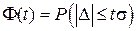Так, для 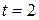по таблице Приложения B находим , а для находим .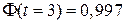

На основании этих теоретических расчетов устанавливают допуски в инструкциях, назначают предельные ошибки по правилу:

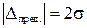(или )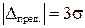

Результаты измерений, у которых ошибки превышают предельную, равную 2s (или 3s), бракуют, и измерения переделывают заново.

Задача 3.1. Найти вероятность того, что ошибка измерений угла D не превзойдёт по абсолютной величине 6,0², если СКО измерений угла равно 10,0², а математическое ожидание ошибок измерений равно нулю (это означает отсутствие систематических ошибок).

Решение: 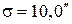и 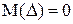— найти 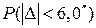. С учётом симметричности пределов 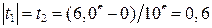и свойства функции 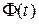, получаем по формуле

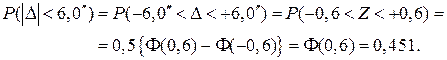
(Значение интеграла вероятностей находим по таблице Приложения B).

Дата добавления: 2014-01-05