Уравнение регрессии

Уравнение линейной регрессии Y на Х, отражающее прямолинейную корреляционную связь между переменными Х и Y, имеет вид:

,

где 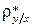— коэффициент регрессии Y на Х, вычисляемый по формуле

.

Задача 5.1. В таблице 5.1 приведены результаты измерений линий D_i (в км) и абсолютные значения ошибок D _i (в см).

Вычислить коэффициент корреляции; с вероятностью 0,90 оценить его надёжность и составить уравнение регрессии D на D.

Прежде чем решать задачу, прибегают к графическому изображению точек .

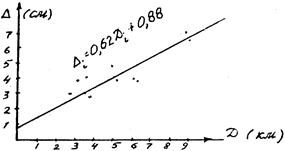
Рис. 5.1 — Прямая регрессии

График на рис. 5.1 указывает на наличие корреляции между D и D.

Решение. Вычисление необходимых сумм, а также контроли вычислений поместим в таблице 5.1.

Таблица 5.1
№ п/п	, км	, см						Примечания
	8,7	6,8	+4,0	+3,0	16,00	9,00	+12,00	1) ; ; . 2) ; ; . 3) ; . Контроль: . Контроль выполнен.
	3,7	3,1	–1,0	–0,7	01,00	0,49	0+0,70
	6,0	3,8	+1,3	–0,0	01,69	0,00	0+0,00
	3,3	2,9	–1,4	–0,9	01,96	0,81	0+1,26
	5,1	4,1	+0,4	+0,3	00,16	0,09	0+0,12
	6,1	3,7	+1,4	–0,1	01,96	0,01	0–0,14
	2,7	2,6	–2,0	–1,2	04,00	1,44	0+2,40
	4,9	4,4	+0,2	+0,6	00,04	0,36	0+0,12
	3,1	2,0	–1,6	–1,8	02,56	3,24	0+2,88
	3,7	4,5	–1,0	+0,7	01,00	0,49	0–0,70
å	47,3	37,9	+0,3	-0,1	30,37	15,93	+18,64

1. Вычисление по формуле, которая в данной задаче примет вид:

;

; ; .

2. Оценка надёжности . Так как число измерений сравнительно небольшое (), для оценки надёжности вычисленного значения коэффициента корреляции применим критерий Фишера, основанный на преобразовании вида:

.

По таблице Приложения C, пользуясь коэффициентом корреляции , как аргументом, находим . Величина подчинена нормальному закону распределения. Доверительный интервал для истинного значения Z имеет вид:

.

определяем по формуле

.

Для вероятности 0,90 по таблице Приложения B находим .

Из таблицы Приложения C находим соответствующие крайним значениям Z значения границ коэффициента корреляции (0,56 и 0,95). Получаем доверительный интервал, с вероятностью 0,90 накрывающий истинное значение r:

.

Так как имеет место соотношение

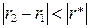(), то прямолинейную корреляционную связь можно считать установленной.

3. Составим уравнение регрессии D на D:

,

;

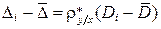приведём его к виду:

;

.

Получаем окончательно:

.

Затем по уравнению строим на графике рис. 5.1 прямую линию.

Достоинство уравнения регрессии состоит в том, что оно позволит по заданным значениям переменной D (в км) предвычислять ожидаемые в среднем значения переменной D (в см).

Дата добавления: 2014-01-05