Коэффициенты вариации

Вариация — это несовпадение значений одной и той же статистиче­ской величины у разных объектов в силу особенностей их собственного развития, а также различия условий, в которых они находятся. Вариация имеет объективный характер и помогает познать сущность изучаемого явления. Если средняя величина сглаживает индивидуальные различия, то вариация, наоборот, их подчеркивает, устанавливая типичность или не типичность найденной средней величины для конкретной статистической совокупности. Тем самым можно делать вывод о качественности подобранных статистических данных.

Вариация измеряется с помощью относительных величин, называе­мых коэффициентами вариации и определяемых в виде отношения среднего отклонения к средней величине.

Поскольку среднее отклоне­ние может определяться линейным и квадратическим способами, то соответствующими могут быть и коэффициенты вариации. Следова­тельно, коэффициенты вариации надо определять по формулам

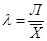– линейный; (1.28)

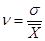– квадратический. (1.29)

Значения коэффициента вариации изменяются от 0 до 1 и чем ближе он к нулю, тем типичнее найденная средняя величина для изучаемой статистической совокупности, а значит и качественнее подобраны статистические данные. При этом критериальным значением коэффициен­та вариации служит 1/3.

То есть средняя величина считается типичной для данной совокуп­ности при λ 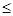0,333 или при ν 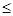0,333. В ином случае средняя величина не типична и требуется пересмотреть статистическую совокупность с целью включения в нее более объективных статистических величин.

Обычно квадратический коэффициент вариации несколько (примерно на 25%) больше линейного, рассчитанные по одним и тем же данным. А значит возможен случай, когда λ 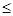0,333 и ν 0,333, тогда необходимо взять среднюю из этих коэффициентов и по ее значению сделать окончательный вывод о не/типичности найденной средней величины.

С помощью линейного коэффици­ента вариации принципиальный вывод о типичности или не типичности средней величины можно получить проще и быстрее, чем с помощью квадратического. Однако квадратический коэффициент применяется чаще, так как существует несколько способов для вычисления дисперсии.

У такого способа оценки вариации есть и существенный недостаток. Действительно, пусть, например, исходная совокупность рабочих, имеющих средний стаж 15 лет, со стандартным отклонением σ = 10 лет, «состарилась» еще на 15 лет. Теперь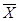 = 30 лет, а стандартное отклонение по-прежнему равно 10. Совокупность, ранее бывшая неоднородной (10/15*100 = 66,7%), со временем оказывается, таким образом, вполне однородной (10/30*100 = 33,3 %).

Поэтому возможен дополнительный анализ статистической сово­купности с помощью коэффициента осцилляции, определяемого по формуле

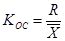, (1.30)

где R — размах вариации в виде разности наибольшего и наимень­шего значений в совокупности статистических величин. То есть

R = Х_мах –Х_min, (1.31)

где X_мax и X_min — максимальное и минимальное значения в совокупно­сти.

При упорядочении статистических величин в совокупности образу­ются группировочные интервалы. Тогда под обозначением ∆Х пони­мается размах интервала, а среднее интервальное значение обозначается Х_И.

В случае ориентировки только на квадратический коэффициент ва­риации могут применяться разные методы определения дисперсии.

Дата добавления: 2014-01-05