
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Методические указания по теме
|
|
|
|
Методику расчета средних величин и коэффициентов вариации рассмотрим на примере группы студентов или слушателей из 21 чел. (N =21), каждый из которых имеет возраст X = 28, 36, 30, 22, 22, 40, 29, 27, 21, 23, 35, 30, 32, 33, 29, 37, 29, 39, 23, 22, 22 лет. Требуется определить средний возраст и установить его типичность или не типичность с помощью линейного и квадратического коэффициентов вариации.
Поскольку данные не упорядочены, то средний возраст определяем по формуле (1.13) как простую среднюю арифметическую величину
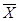 = (28+36+30+…+23+22+22)/21 = 29 лет.
= (28+36+30+…+23+22+22)/21 = 29 лет.
Для применения формулы средней арифметической взвешенной выполним первичную (дискретную) группировку данных, расположив их в порядке увеличения возраста и определяя повторяемость, встречаемость или частоту одинакового возраста, как показано в табл. 1.1.
Таблица 1.1
Первичная или дискретная группировка данных
| Xi | 
| ||||||||||||||
| fi |
Тогда по формуле (1.14) средний возраст будет равен
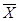 = (21*1+22*4+23*2+…+37*1+39*1+40*1)/21 = 29 (лет).
= (21*1+22*4+23*2+…+37*1+39*1+40*1)/21 = 29 (лет).
Хотя результат и оказался одинаковым, но первичная группировка дает более четкое представление о структуре статистической совокупности. В данном примере это возрастная структура группы студентов. К тому же, она позволяет перейти к определению линейного коэффициента вариации.
Так, по формуле (1.23) среднее линейное отклонение взвешенное равно
Л = 4,857 лет
а линейный коэффициент вариации по формуле (1.28) равняется
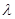 = 4,857/29 = 0,168
= 4,857/29 = 0,168
Вывод: средний возраст 29 лет является типичным для рассмотренной группы студентов, т.к. расчетный коэффициент вариации оказался меньше его критериального значения (0,168 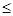 0,333).
0,333).
Дополнительно определяется коэффициент осцилляции, для чего предварительно по формуле (1.31) находим размах вариации
R = 40-21 = 19 (лет).
Значит, по формуле (1.30) коэффициент осцилляции равняется
Кос = 19/29 = 0,655.
Для нахождения квадратического коэффициента вариации выполним вторичную (интервальную) группировку данных, используя формулу Стерджесса для определения оптимального количества интервалов п. Эта формула имеет вид
n = 1 +3,322 lg N, (1.33)
позволяя затем находить необходимый размах интервала как отношение
 Xи = R / n. (1.34)
Xи = R / n. (1.34)
Подставляя данные примера в эти формулы, находим количество интервалов n =1+ 3,322 lg 21 = 1+3,322*1,322 = 5,4. Так как количество интервалов не может быть дробным, то его нужно округлить до ближайшего целого числа (по правилам округления). То есть нужно принять 5 интервалов.
По формуле (1.32) размах интервала будет равен 19/5 = 3,8, то есть 3,8 года. Интервальная группировка данных приведена в первом столбце табл. 1.2, которая содержит также алгоритм и промежуточные расчеты.
Таблица 1.2 Промежуточные расчеты по интервальной группировке данных
| Xi, лет | fi | ХИ | XИfi | ХИ-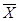
| (ХИ-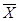 )2 )2
| (ХИ-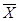 )2 fi )2 fi
|
| до 24,8 | 22,9 | 160,3 | -6,333 | 40,111 | 280,7778 | |
| 24,8-28,6 | 26,7 | 53,4 | -2,533 | 6,418 | 12,83556 | |
| 28,6-32,4 | 30,5 | 1,267 | 1,604 | 9,626667 | ||
| 32,4-36,2 | 34,3 | 102,9 | 5,067 | 25,671 | 77,01333 | |
| 36,2-40 | 38,1 | 114,3 | 8,867 | 78,618 | 235,8533 | |
| Итого | — | 613,9 | — | — | 616,1067 |
В табл. 1.2 первый и последний интервалы открытые, не имея нижней или верхней границы диапазона, а промежуточные интервалы закрытые, имея обе границы. Нахождение середин закрытых интервалов затруднений не вызывает, а с открытыми интервалами поступают следующим образом: к открытому интервалу применяют размах соседнего (смежного), но так как размах всех интервалов в нашем примере одинаков и равен 3,8 года, то и здесь затруднений не должно быть.
У первого интервала отсутствует нижняя граница и находят ее путем вычитания размаха смежного интервала из имеющейся верхней границы, получая тем самым закрытый интервал, середина которого определяется легко. В данном примере имеем 24,8–3,8 = 21 год, значит, середина этого интервала будет равна (21+24,8)/2 = 22,9 года.
У последнего интервала отсутствует верхняя граница и находят ее путем прибавления размаха смежного интервала к имеющейся нижней границе, получая тем самым также закрытый интервал. В данном примере имеем 36,2+3,8 = 40 (лет), значит, середина интервала 36,2-40 будет 38,1 лет.
По итогам табл. 1.2 определяются такие характеристики, как средний возраст по формуле (1.14)
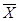 = 613,9/21 = 29,2333 (лет).
= 613,9/21 = 29,2333 (лет).
Как видим, результат несколько отличается от предыдущего, что вызвано неизбежным округлением расчетного количества интервалов. Чем больше количество интервалов и меньше их размах, тем меньше будет разница в результатах.
Затем по формуле (1.25) определяется взвешенная дисперсия отклонений
Д = 616,1067/21=29,3384 лет2.
Далее по формуле (1.26) находится среднее квадратическое отклонение
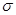 =
= = 5,4165 лет.
= 5,4165 лет.
И, наконец, по формуле (1.29) рассчитывается квадратический коэффициент вариации
 = 5,4165 /29,2333 = 0,185.
= 5,4165 /29,2333 = 0,185.
По значению этого коэффициента делается вывод о типичности среднего возраста 29,23 лет для рассмотренной группы студентов, т.к. расчетное значение коэффициента вариации не превышает критериального (0,185 < 0,333).
Рассмотренный пример подтвердил возможность одинаковых выводов о типичности или не типичности средней величины с помощью линейного и квадратического коэффициентов вариации и показал, что приход к конкретному выводу осуществляется значительно проще и быстрее с помощью линейного коэффициента.
|
|
|
|
Дата добавления: 2014-01-05; Просмотров: 408; Нарушение авторских прав?; Мы поможем в написании вашей работы!