Геометрия цилиндрических зубчатых передач

Зубчатые передачи.

Передачи.

Лекция №2

ЗП – это механизм, который с помощью зубчатого зацепления передает или преобразует движение с изменением угловых скоростей и моментов. Передача вращательного движения осуществляется с помощью последовательно зацепляющихся зубьев. Тела вращения, на которых расположены зубья, называют зубчатыми колесами. Меньшее колесо зубчатой пары называется шестерней, а большее – колесом. Собственно колесо состоит из диска со ступицей и зубчатого венца.

ЗП применяют для преобразования и передачи вращательного движения между валами с параллельными, пересекающимися и скрещивающимися осями, а также для преобразования вращательного движения в поступательное и наоборот. ЗП между параллельными валами осуществляется цилиндрическими колесами с прямыми, косыми и шевронными зубьями (рис. 1 а-г). Если передача образована парой зубчатых колес, зубья которых нарезаны на наружной поверхности колеса, то имеет место внешнее (наружное) зацепление. Когда зубья одного из колес зубчатой пары нарезаны на внутренней поверхности, а другого – на наружной, то зацепление считается внутренним. Зубчатые колеса различаются по форме рабочей поверхности зуба (профилю зуба). Наибольшее распространение получили в машиностроении зубчатые колеса с эвольвентным зацеплением.

Передачи между валами с пересекающимися осями осуществляются обычно коническими колесами с прямыми, косыми и тангенциальными зубьями. ЗП для преобразования вращательного движения в поступательное и наоборот, осуществляются цилиндрическим колесом и рейкой. Для валов с перекрещивающимися осями применяют зубчато-винтовые передачи.

+: 1. Малые габариты. 2. Высокий КПД. 3. Большая надежность в работе. 4. Постоянство передаточного отношения. 5. Возможность применения в широком диапазоне моментов, скоростей и передаточных отношений.

-: 1. Требования высокой точности изготовления. 2. Шум при работе.

Профиль зуба зубчатого колеса очерчен участком эвольвенты окружности, которая представляет собой кривую, центры кривизны которой принадлежат рассматриваемой окружности. Эвольвента может быть получена как траектория точки прямой t-t, перекатывающейся без скольжения по этой окружности радиусом r_b называемой основной окружностью.

На рис. изображен контакт двух эвольвент окружностей, проведенных радиусами r_b1 и r_b2 из центров О₁ и О₂. При вращении звеньев 1 и 2 точка касания эвольвент перемещается вдоль отрезка АВ. То есть, для колес с эвольвентным зацеплением геометрическое место точек контакта профилей зубьев при вращении представляет собой прямую. Эвольвента – единственная известная в математике кривая, обеспечивающая прямую линию зацепления.

Точка пересечения общей нормали к эвольвентам с межосевой линией называется полюсом зацепления Р. Окружности радиусами О₁ Р и О₂ Р называются начальными окружностями (делительными окружностями). Диаметры начальных окружностей колес обозначим через d_w1 и d_w2 (радиусы, соответственно, r_w1 и r_w2), положение нормали к поверхности определяется углом зацепления 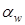=20⁰.

Эвольвентный профиль зацепления обеспечивает постоянство передаточного отношения, так как при передаче постоянного момента нормальная сила в контакте двух эвольвент неизменна по величине и направлена вдоль линии зацепления (см. рис).

Основные параметры: шаг зацепления, модуль зацепления (ряды модулей приведены в ГОСТ), диаметры делительной окружности, выступов зубьев и впадин зубьев, межосевое расстояние.

Колесо, зуб которого наклонен под углом 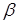к оси вращения, называется косозубым. Два косозубых колеса с противоположным направлением зубьев образуют шевронное колесо. Прочность косозубых и шевронных колес выше, чем прямозубых, за счет увеличения осевой длины контакта, причем, чем больше угол наклона зуба, тем колесо прочнее. С другой стороны, увеличение угла вызывает значительные осевые нагрузки, поэтому для косозубых колес рекомендуется 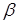=8…15⁰. Для шевронных колес, у которых осевые нагрузки скомпенсированы противоположным направлением зубьев, 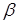=30…45⁰. Различают модуль нормальный, измеренный перпендикулярно линии зуба (m_n) и окружной (торцевой) модуль, измеренный в торцевом сечении (m_t). В качестве расчетных параметров принимают параметры торцевого сечения.

Наиболее опасной причиной разрушения зубчатых колес является поломка зуба, вызванная его изгибом. Этот вид разрушения носит усталостный характер, начинается с зарождения трещины в наиболее напряженной части: у основании зуба в зоне растяжения. Размеры трещины увеличиваются и достигают таких значений, при которых происходит скол части зуба или излом. Для предотвращения этого зубья колеса рассчитываются на изгибную прочность.

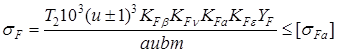
Т - крутящий момент на ведомом колесе;

u – передаточное число зубчатой передачи;

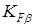- коэффициент концентрации нагрузки;

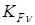- коэффициент динамичности нагрузки;

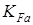- коэффициент неравномерности нагружения зубьев;

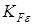- коэффициент перекрытия зубчатой передачи;

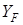- коэффициент формы зуба (геометрический параметр);

а - межосевое расстояние передачи;

b­ – ширина зуба;

m – модуль передачи;

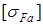- допускаемое напряжение усталостной прочности на изгиб.

Еще одной причиной разрушения зубчатых колес является выкрашивание контактной поверхности зубьев. Характерен для передач, работающих в условиях обильной смазки, сначала возникает трещина на контактной поверхности, а затем начинается отслаивание локальных участков контактирующих поверхностей. Для предотвращения этого проводят проверку контактной прочности передачи.

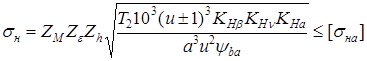
где 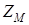- постоянная, зависящая от материала колес;

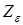- к-т, учитывающий влияние торцевого перекрытия на величину напряжения в контакте;

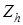- параметр геометрии зацепления;

Т₂ – крутящий момент на ведомом зубчатом колесе;

u – передаточное число зубчатой пары;

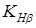- коэффициент концентрации нагрузки;

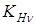- коэффициент динамичности нагрузки, учитывающий точность изготовления зубчатых колес и скорость их вращения;

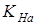- коэффициент неравномерности нагружения зубьев при расчетах по контактным напряжениям;

а ­ – межосевое расстояние;

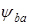- коэффициент ширины зубчатого зацепления;

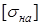- допускаемое контактное напряжение.

Дата добавления: 2014-01-05